


Up: tawami
Previous: たわみの基礎方程式
- 曲率とモーメントの関係
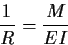 |
(1.5) |
と,はりのたわみに関する幾何学的な考察から得られる次の3つの関係式を使うことではりの基礎方程式を導くことができる.
- たわみ角とたわみ曲線の勾配
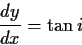 |
(1.6) |
- 微小線素
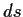 ,
,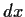 とたわみ角の関係
とたわみ角の関係
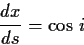 |
(1.7) |
- 曲率半径
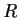 と微小線素
と微小線素 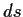 の関係
の関係
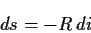 |
(1.8) |
式(1.8)から
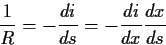 |
(1.9) |
上式に式(1.7)を代入
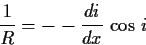 |
(1.10) |
一方,式(1.6)を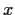 で微分して
で微分して
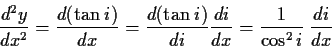 |
(1.11) |
したがって
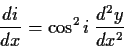 |
(1.12) |
式(1.10)に上式を代入すれば
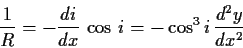 |
(1.13) |
たわみ角 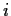 が微小(
が微小(
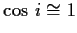 )であることと考慮すると,曲率半径は以下のように近似できる.
)であることと考慮すると,曲率半径は以下のように近似できる.
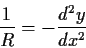 |
(1.14) |
すなわち式(1.5)に上式を代入すれば,たわみの基礎方程式
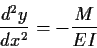 |
(1.15) |
が得られる.



Up: tawami
Previous: たわみの基礎方程式
By Shigeru NAGAKI updated 2004/04/21
![]() が微小(
が微小(
![]() )であることと考慮すると,曲率半径は以下のように近似できる.
)であることと考慮すると,曲率半径は以下のように近似できる.