General Model of Growth
経験的に何気なく認識している人も多いとは思いますが,「成長」する姿勢に基づいて何らかの活動する人として定義される「学生」にとって重要な,知的活動の能力に関する成長の一般的な特徴を2つ述べておきます.
1つは,成長する意思の重要性です.運動方程式を例えにして説明しましょう.現在,何かができるかどうかという状態を「位置」に相当させます.すると,できるようになりつつあるのは「速度」に相当します.さらに,そのために自分がどう取り組むのかという,行動に直結した意思は,運動方程式における「加速度」に相当します.御存知の通り,Newtonの運動方程式では質量を通じて加速度は「力」と関係づけられます.高い意識というポテンシャルを通じて力強く成長してほしいです.運動方程式の解において,長期的に重要なのが何か考えてもらえれば,その意思の大切さも容易に理解できるでしょう.
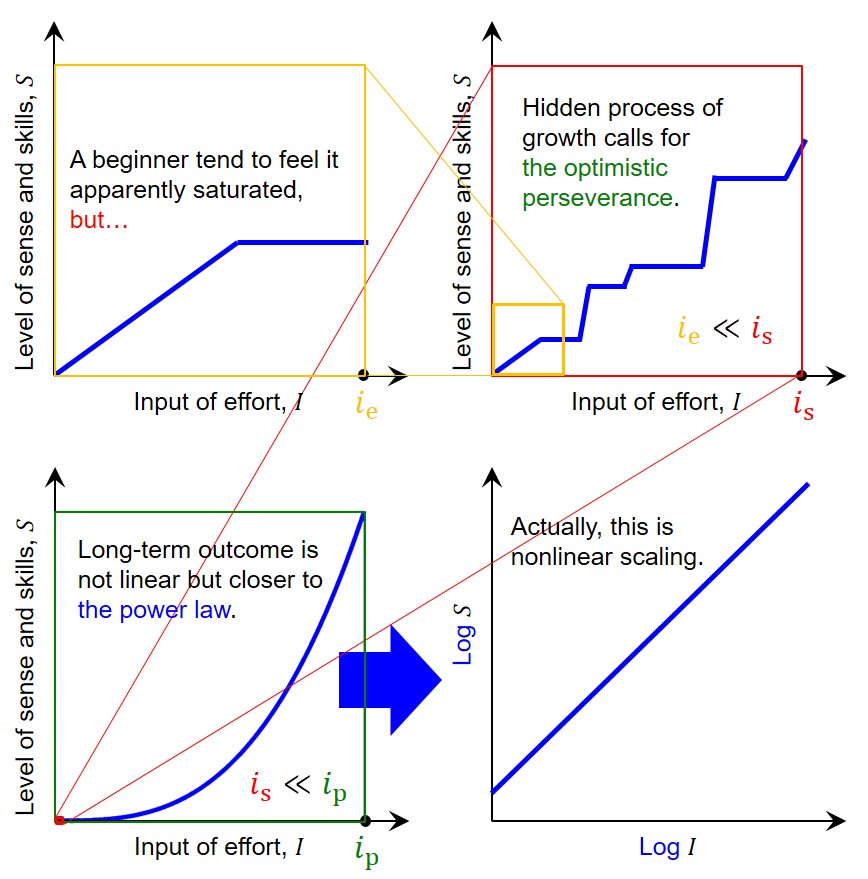
もう1つは,仮に成長に関する運動方程式を解いた場合の一般解の形の特徴です.充分な経験の蓄積を経てレベルアップするという特徴は,物理現象における「相転移」のようなものです.一例として,氷を温める(つまり熱エネルギーを入力する)と,常圧では0℃になるまで温度上昇するというわかりやすい変化がありますが,融けて水になる相転移の際には温度変化があません.トレーニングを通じて成長する際も,自他ともに変化がわからない段階がしばらく続くのが自然なことです.この段階で諦めず継続的に努力することで,初めてレベルアップできます.さらに,これを繰り返して長期継続的な成長が実現します.
このような成長の過程をグラフに表そうとした場合,横軸に努力している量のようなものを取って,縦軸に能力のようなものを取れば,階段状に見えることになります.これが繰り返されたものは,細かく見るとギザギザしていますが,遠目ではどう見えるでしょうか?敢えて単純化して言えば,指数が1より大きなべき乗則のように見えるのが一般的です.つまり,両対数で見れば右肩上がりの線形ですが,実際にできることの能力をつぶさに見れば飛躍的な上昇です.それは横軸の範囲を大きく確保するほど劇的な変化です.的確に取り組んで博士後期課程を修了した暁には,成長して次元の異なる視野と能力が身に付きます.
人間は多様なので,ここで例えとして述べたグラフの軸には,必ずしも縦軸と横軸を対応付ける便利な数値の目盛がありません.単純なスキルは目盛も付け易いですが,わざわざ学生が大学で培うことを狙うような地力は,簡単に代わりの利く陳腐なものではありません.ですから,日常を継続的に前向きに過ごす意思の力が大切です.理性と感情を統御して行動につなぐ意思です.むしろ,成長だけを意識していると自意識過剰でつらいでしょう.研究室での生活は,世界に直結した社会の中で科学技術を担う現場での活動ですから,むしろ客観的に認識し得る側面に集中していれば,やがて後から成長が付いてくるという理想的な構図を確保できます.