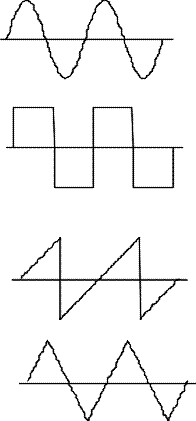
�ȉ��́A���`�g�A�O�p�g�A�S�g�����g�A�ڌv�Z���邽�߂̊��������܂��B���Ԃ��]�����l�́A���K���11-4�̃R�T�C���g�𑫂����킹�č�����g�`�f�[�^�Ɣ�r���Ă݂Ă��������B
/* ���`�g�f�[�^�̌v�Z*/
void make_rectwave(int len, float freq,float tdel,float amp,float *x)
{
int i;
float arg,time;
for(i=0;i<len;i++){
time=tdel*i;
arg=fmod(freq*time,1.0);
if(arg==0.0 || arg==0.5)
x[i]=0.0;
else if(arg<0.5)
x[i]=amp;
else
x[i]=-amp;
}
}
/* �O�p�g�f�[�^�̌v�Z*/
void make_triwave(int len, float freq,float tdel,float amp,float *x)
{
int i;
float arg,time;
for(i=0;i<len;i++){
time=tdel*i;
arg=fmod(freq*time,1.0);
if(arg<=0.25)
x[i]=4.0*amp*arg;
else if(arg<=0.75)
x[i]=4.0*amp*(0.5-arg);
else
x[i]=4.0*amp*(arg-1.0);
}
}
/* �S�g�����g�f�[�^�̌v�Z*/
void make_fulwavrec(int len, float freq,float tdel,float amp,float *x)
{
int i;
float arg,time;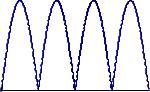
for(i=0;i<len;i++){
time=tdel*i;
x[i]=fabs(sin(2.0*PI*freq*time));
}
}
/* �̂�����g�f�[�^�̌v�Z*/
void make_sawtoothwave(int len, float freq,float tdel,float amp,float *x)
{
int i;
float arg,time;
for(i=0;i<len;i++){
time=tdel*i;
arg=fmod(freq*time,1.0);
if(arg<0.5)
x[i]=2.0*amp*arg;
else if(arg==0.5)
x[i]=0.0;
else
x[i]=2.0*amp*(arg-1.0);
}
}