Collective dynamics of chemical oscillators
Belousov-Zhabotinsky reaction
The Belousov-Zhabotinsky (BZ) reaction is a chemical reaction that exhibits periodic changes and complex patterns. The concentration of several reactants changes periodically during the reaction, so the BZ reaction is widely known as one of an oscillating reaction. When the BZ reaction solution is well stirred, the periodic behavior can be observed as a color change of the solution. In a thin layer, propagating chemical wave can be observed. These are surely the dissipative structures, which can be seen in the living system such as cardiac rhythm and animal coat patterns. Because of similarities to the living system, the BZ reaction is widely studied not only in chemistry but also in biology, physics, and mathematics.
BZ oscillators
We constructed the discrete BZ reaction system using photolithography-assisted techniques. This methodology allowed the fabrication of the reactor with two-dimensionally arranged, microsized units. The reactor was made from the elastometric material poly(dimethylsiloxane) (PDMS). The catalyst of the BZ reaction, Ru(bpy)32+, was immobilized in silica-gel matrices. We look on a catalyst-doped microgel element in a reactor unit as an oscillator. The reactor was placed into a chamber that was continuously fed with fresh catalyst-free BZ solution to maintain constant nonequilibrium conditions. In this system, the coupling between oscillators is accomplished via a mass diffusion. In the following movie, all oscillators behave like independent oscillators because of weak coupling.

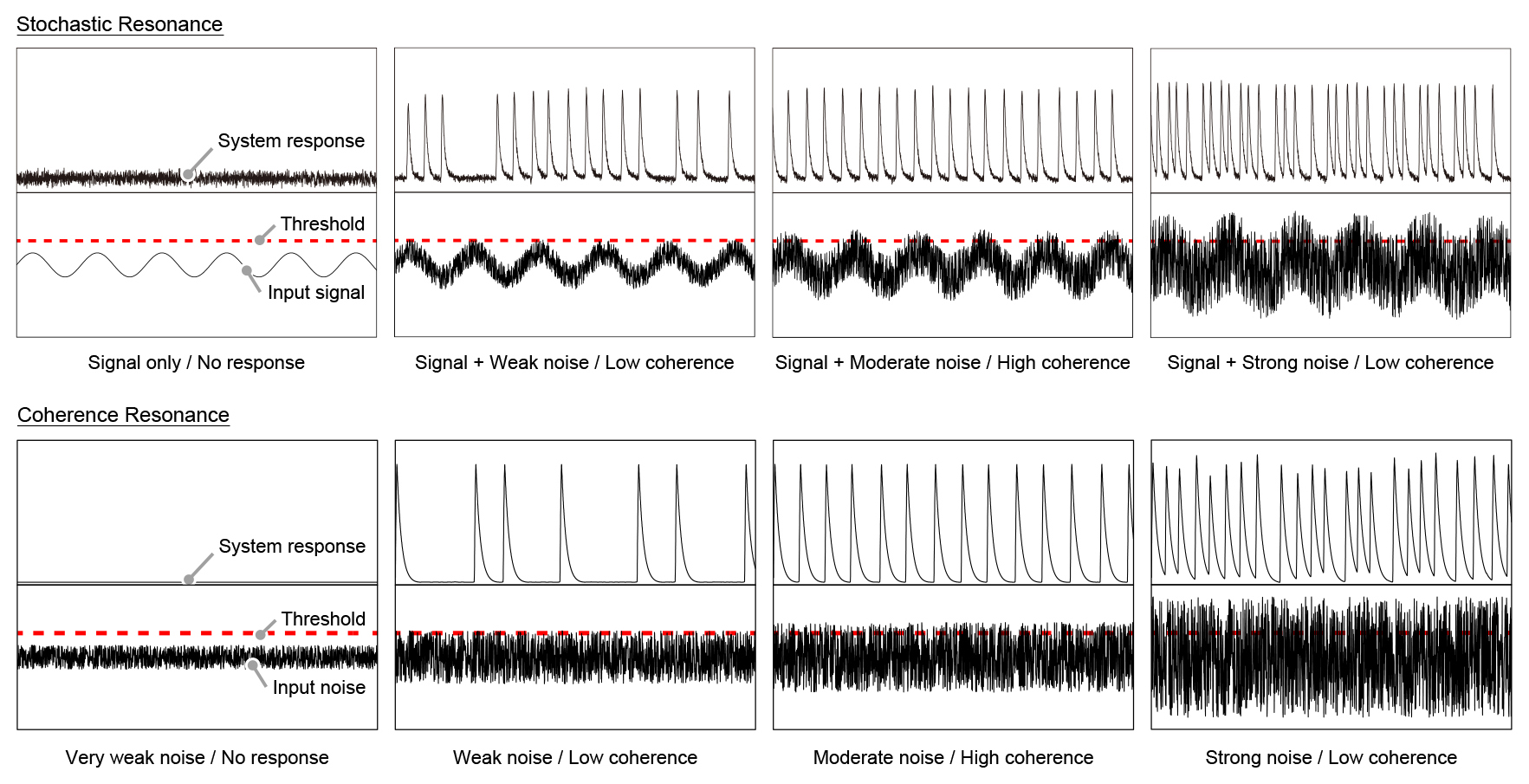
Array-enhanced coherence resonance
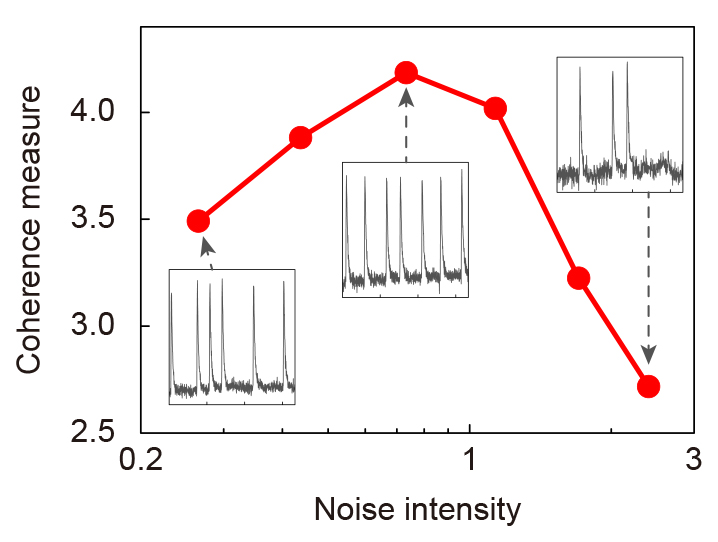
Nontrivial effects of noise in nonlinear systems have recently attracted much attention. One of the most interesting effects is stochastic resonance, which is characterized as an enhancement of a system response to a weak periodic input signal due to a moderate noise intensity. Even in the system without external periodic forcing, the coherence of system responses is enhanced for an optimal noise intensity, called coherence resonance (CR). The phenomenon of CR has been experimentally confirmed in various systems.
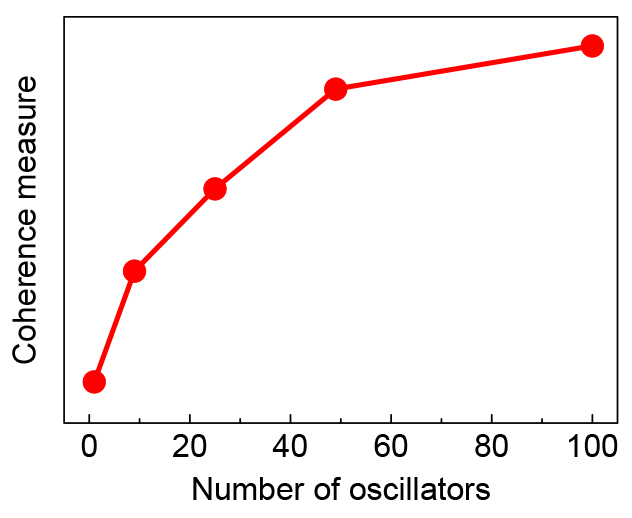
We experimentally and numerically demonstrated that in a two-dimensional array of BZ oscillators subjected to independent external noise, the coherence of system responses is improve with increasing the array size, i.e., the occurrence of array-enhanced coherence resonance (AECR). This result indicates that the interplay between noise and interactions among oscillators is crucial for noise-enhanced resonance. However, observed array-enhanced effects tend to saturate for a further increase of the number of oscillators beyond 100.
Feedback-controlled dynamics
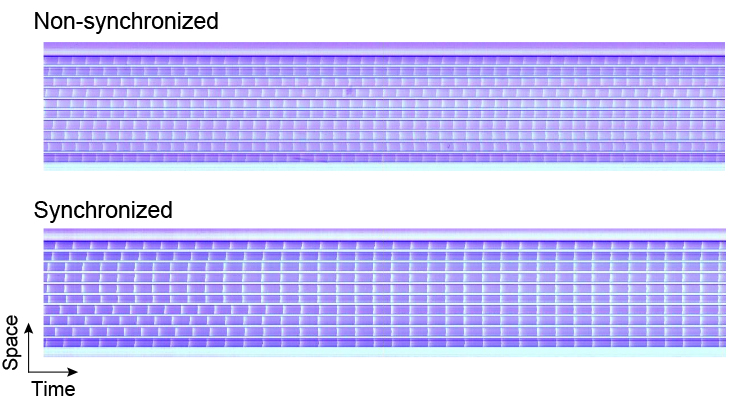
When many elements capable of autonomous oscillation are coupled, cooperative interactions among them reveal complex but ordered collective dynamics behaviors as basic manifestations of self-organization. The most significant of these patterns are synchronization and clustering that are frequently observed in physical, chemical, and biological systems. In inducing these behaviors, a coupling scheme between oscillators is essential. Feedback techniques allow each oscillator to interact with any other oscillator in the array. This offers possible approaches for designing desired interactions among oscillators.
In order to investigate the effect of different coupling schemes, we introduced a feedback control to an array of BZ oscillators. The feedback was achieved by monitoring the reaction of oscillators, processing its image by computer, and illuminating the signal on the oscillator array.
First, we investigated the effect of time-delayed feedback on spatial dynamics in a globally coupled oscillator array. We found that, when the delay time is optimal, phase synchronization is induced at the feedback gain more than a threshold value. We revealed that the spatiotemporal coherence of oscillations can be effectively controlled by varying feedback parameters, such as the delay time and the gain.
The effect of adaptive coupling on spatial dynamics was also investigated. The adaptive coupling is achieved by the feedback force that changes depending on the relative phase between the oscillators. We found that depending on the form of the adaptation function, the system undergoes two- or three-cluster synchronization. In the results described above, global synchronization was observed at an appropriate delay time, but not cluster formation. Thus, adaptive coupling is essential for the cluster formation in the discrete system.

Collective dynamics of chemical oscillators
Deformation of giant unilamellar vesicles

Protein synthesis from a single copy of DNA

Volume dependence of protein synthesis

Droplet & Microchannel
(Paper in progress)

Impact sensor
(Ring!Ring!Project)