Google Scholarのトップページに「巨人の肩の上に立つ」という言葉が掲げられている。「偉大な先人の積み重ねた発見や研究などを『巨人』に例えて,現在の学術研究の新たな知見や発見,学問の発展も,それらの積み重ねの上に成り立っている」という意味のようだが、元を辿ってみると、”If I have seen further it is by standing on the shoulders of giants.”というアイザック・ニュートンの書簡という話もあるが、最初に用いたのは12世紀のフランスの哲学者、Bernard de Chartresとされる。” Bernard of Chartres used to say that we [the Moderns] are like dwarves(小人、矮人) perched on the shoulders of giants [the Ancients], and thus we are able to see more and farther than the latter. And this is not at all because of the acuteness of our sight (視覚が鋭敏であること) or the stature of our body, but because we are carried aloft and elevated by the magnitude of the giants.”
大学での教育・研究活動の中で、現在の学問体系、あらゆる分野におけるテクノロジーは、先人達の天才的なひらめきと途方もない努力の上で成立していることを忘れてはいけないし、学生諸氏にはそのことを伝承していかなければならない・・・。
例えば、ポリビニルアルコールのところで紹介した、Paul J. Floryのアセタール化の割合の話は、1939年の論文が元ネタである。Staudingerが唱えた“高分子説”が受け入れられたのは1930年ころといわれているが、その9年後に高分子を統計的に取り扱う論文が出ていることは驚くべきことのように思う。
「故(ふる)きを温(たず)ねて新しきを知る」ということで、何回かに分けて先人の偉業を紹介し、敬意を表してみたいと思う。
今回は日本の初の女性化学者といわれる黒田チカ先生の偉業について・・・・。黒田先生は女子高等師範学校(お茶の水女子大学の前身)を卒業後、母校の助教授を経て、初めて帝国大学に入学した女性である(経歴等はココに詳しい)。東北帝国大学3年次に、漆の主成分であるウルシオールの構造決定と合成を行った真島利行先生の研究室で指導を受けることになった。真島教授との協議の上、ムラサキ草の根(紫根)から抽出される染料の構造決定をテーマとした(紫は昔から洋の東西を問わず格式高い色として珍重されていた)。多くの研究者が取り組んだようだが、熱に弱く、純粋な結晶として単離されていなかった。具体的な実験の内容は下記の通りである(黒田チカ,東京化学会誌,39,1051-1115 (1918)、C. Kuroda, R. Majima, Acta Phitochimica, 1, 43-65 (1922).)。
紫根30 kg を室温でベンゼンにより抽出し,抽出液を40 ℃下で濃縮→約1.2 kg の赤紫色のシロップを石油エーテルで処理し,可溶部から約700 g のシロップをゲット。水酸化ナトリウム水溶液で処理した後、硫酸で酸性にし,結晶性物質435 g を得た。ベンゼンから再結晶すると融点147 ℃の紫褐色の結晶。元素分析によると C16H1605 でシコニン(shikonin)と命名。構造決定のための情報は下記の通りである。
①呈色反応からフェノール性物質であった
②40 ℃と低温で,数週間かけるとトリアセチル誘導体をゲットできた→水酸基が3 個存在する
③トリアセチル誘導体をオゾン化し,種々の処理(オゾン分解)の後に3,6-ジヒドロキシフタル酸(既知物)の結晶と,コハク酸及びアセトンが得られた
④シコニンの亜鉛末蒸留によって微量のナフタレンを得た
⑤ナフタレン環に結合した側鎖の構造は鮫の肝油の不飽和化合物(スクワレン)のオゾン分解物(真島研究室の久保田勉之助氏の研究)と比較して決定
この結果と紫外可視吸収スペクトルより、以下のような構造式が推定した。
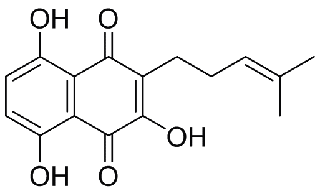
(当初、推定された構造)
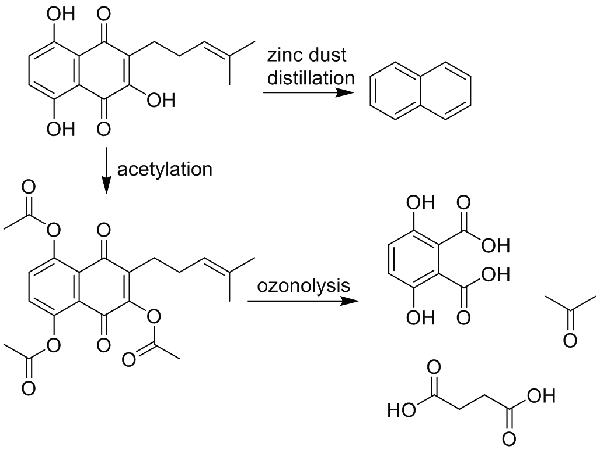
(さまざまな反応)
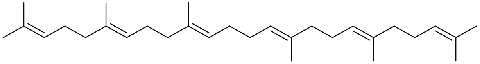
(スクアレンの構造、オゾン分解でアセトンとコハク酸が生成)
最初の石油エーテルの可溶部分のシロップを,1 年以上放置した中からシコニンのモノアセチル誘導体が結晶として析出した。紫根の中でシコニンはこの形で存在することが明らかになった。
その後、シコニンには旋光性があることがわかり、下記のように構造が訂正された。
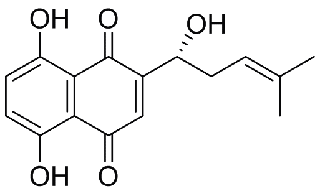
現在、有機化合物の構造決定をする場合、各種のクロマトグラフィー、核磁気共鳴(NMR)スペクトル、赤外可視吸収スペクトルなどから、総合的に判断ということになる。それらが使えず、精製法も確立していなかった時代に、構造決定する難しさに関しては、我々のように、曲がりなりにも日常的にそれをやっている人間には痛いほどよくわかる話である。さまざまな反応を行い、それらの生成物を既知物質と比較し、そこから得られた知見を元に、その構造を推定していくと作業は、途方もないものであり、実際、2年もの歳月を要した。ただ、真島教授が所有していた日本で唯一のオゾン分解装置(ウルシオールの不飽和の部分の構造決定にとても有用)が、威力を発揮したことは確かですね。
「物に親しむ,物が全てを教えてくれる」という黒田先生の座右の銘、私を含めて化学を生業とするものにとって、心に沁みる言葉ですなー。
おまけ(球面三角形の面積の問題です。これはマニアックな題材で直感的にできますが、奥は深いです)
球面S上で2つの大円C1、C2(球の中心を通る平面と球面との交線のこと)が点Pで交わっているとする。点PのおけるSの接平面をα、C1を含む平面をα1、C2を含む平面をα2とし、αとα1、αとα2の交線をそれぞれl1、l2とする。このときS上で2つの大円C1とC2が点Pにおいてなす角を、α上でのl1、l2のなす角として定義する。
下図のように半径1の球面上で大円の弧AB、BC、CAが球面三角形を作っている。上記の定義に従って、その内角の大きさを∠A、∠B、∠Cとするとき球面三角形ABCの面積を求めなさい。
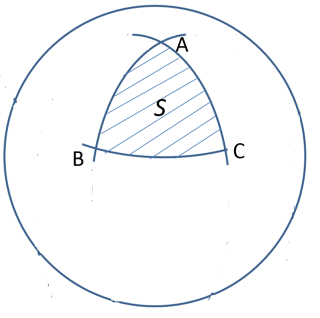
解答例
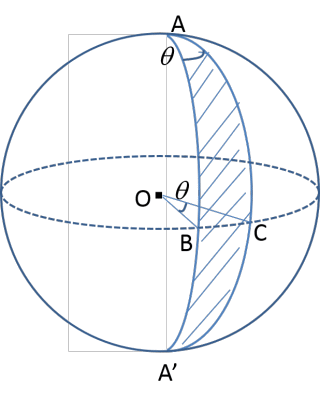
まず、下図のように半径1の球面上で2つの大円が角θをなして交わっているとき、斜線部の面積をθで表すと・・・
2つの大円の交点をA、A’とするとAとA’は球の中心Oにたいして対称である。Oを通り、AA’に垂直な平面と大円の弧との交点をB,Cとすると、平面BOCは点A、A’での接平面と平行になる。したがって、上記の定義を考えると∠BOC=θとなる。下図の斜線部の面積は球の表面積(4πr2=4π)のθ/2πであるから、2θとなる。
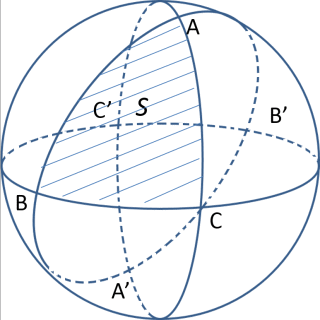
次に下図の通り、A、B、Cの球の中心に対しての対称点をそれぞれA’、B’、C’とすると
S+△BCA’=2∠A
同様に、
S+△CAB’=2∠B
S+△ABC’=2∠C
辺々を足し合わせると、2(∠A+∠B+∠C)=3S+△BCA’+△CAB’+△ABC’ ①
また、△ABCの面積と△A’B’C’は等しく、形状ABA’Cの面積と形状AB’A’C’の面積は等しい(2∠A)ので、△BCA’=△AB’C
したがって、S+△BCA’+△CAB’+△ABC’=S+△AB’C’+△CAB’+△ABC’=2π(半球の表面積)。∴△BCA’+△CAB’+△ABC’=2π-Sとなり、これを①に代入すると
S=∠A+∠B+∠C-πとなる(答)
(球面三角法と呼ばれる幾何学の一分野のとっつきとなる問題で、実用上は緯度経度が既知の2つの地点の距離を見積もることなどに利用されます。余力があったら追記したいと思います)
(2019.7.15)