実用金属円管材の弾塑性変形特性評価と材料モデリング

　研究の背景・目的

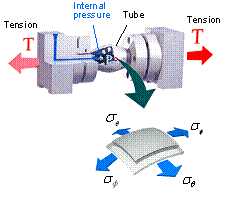
　現代社会では，自動車は生活の手段として欠かせない．しかし一方で，自動車台数の増大は，排出ガスに含まれるCO2による地球温暖化，石油資源の枯渇など，地球環境保存のうえで大きな問題を抱えている．この対策として，車体の軽量化技術による燃費向上が渇望されている（車体重量が10%軽くなると，CO2排出量は約5%低減される）．
　車体の軽量化技術として最も注目されている加工技術がチューブハイドロフォーミングである．チューブハイドロフォーミングとは，図１に示すように，直管を曲げ，金型に挿入した後，軸力を負荷しつつ高圧の液体で円管を膨張させて金型形状を転写し，所望の形状の中空部品を製造する塑性加工法である．利点として，部品の中空化による軽量化，高剛性化，材料の加工硬化による高強度化，部品の一体化によるコストダウン効果など，さまざまな効果がある．　

　チューブハイドロフォーミングの普及の妨げとなっている要因のひとつとして，成形可否（管材の破断）の予測が難しいことが挙げられる．この原因として，①材料が複雑な変形履歴をたどること，②新しい成形技術であるため，加工のノウハウがほとんどない，ことがあげられる．そのため，加工条件や金型形状の検討は試行錯誤で行われているのが現状である．この対策として，有限要素法による成形シミュレーションの活用があるが，実用管材（φ40～80mm，肉厚2～4mm）の塑性変形特性を表現するための材料モデルはほとんど解明されておらず，信頼性のある成形シミュレーションを実現するまでに至っていない．
　そこで本研究では，自動車軽量化用材料として有望視されている高強度鋼管および成形性に優れる高成形性鋼管を対象として，次の二項目を解明することを研究目的とする．

①	二軸応力下における塑性変形挙動の詳細測定と定式（材料モデリング）
②	線形応力経路および複合応力経路における破断時期予測手法（成形限界応力線）の確立

図1　チューブハイドロフォーミングの加工工程

　研究方法と特徴

　以上の技術ニーズを鑑み，当研究室では，実際のチューブハイドロフォーミングにおいて実際に使われている実用金属円管（鋼管，アルミニウム合金管など）を研究対象として、その弾塑性変形特性を高精度に測定するとともに，最適な異方性降伏関数を用いてその塑性変形挙動を定式化（材料モデリング）するための，高精度な二軸引張応力試験機を開発した（図２）．
　本試験機の特長は，①サーボ制御フィードバック回路により，円管に作用する応力経路もしくはひずみ経路を任意に制御する機能を有する，②最大荷重200kN，最大内圧60MPaと大出力であるため，自動車用大型円管の高精度な材料試験が可能である．部品の一つに至るまですべて当研究室で設計した試験機であるが，実用円管の材料試験機としては世界最高性能を有する．
　本研究により自動車車体の軽量化が推進されれば，地球環境の保全に多大な寄与となる．また，金属材料の塑性変形特性の解明およびモデリング手法が新たに確立され，塑性力学の新たな進展に貢献するものと確信する．

図2　実用金属円管用サーボ制御二軸応力試験機

　研究成果

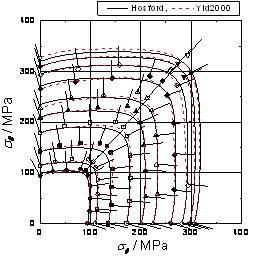
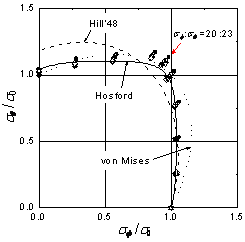
　実験方法として，管軸方向応力と円周方向応力の比率を一定に保持した線形二軸応力経路を供試材に付与し，管軸方向および円周方向の応力ひずみ曲線を測定する．次に測定された応力ひずみ曲線から，単位体積当たりに消費された塑性仕事を求め，等塑性仕事面を求める．そして，代表的な異方性降伏関数による計算値と比較することにより，本供試材に最も適した異方性降伏関数を同定する．
　一例として，アルミニウム合金管の二軸応力試験において測定された等塑性仕事面の測定結果と各種降伏関数による計算値を比較した結果を図３に示す．本実験では，応力経路を=1:0, 4:1, 2:1, 4:3, 1:1, 20:23, 3:4, 1:2, 1:4, 0:1の10通りとした．応力比20:23は，本供試材の塑性ひずみ増分ベクトルの比がほぼ1:1になる応力比である．塑性仕事と塑性流動応力の関係式としては，管軸方向の単軸引張試験から得られた真応力－対数塑性ひずみ曲線を基準とした．すなわち，管軸方向の単軸引張試験において，管軸方向の対数塑性ひずみが既定値に達するまでになされた単位体積当たりの塑性仕事Wを測定し，他の応力比においては，Wと等量の塑性仕事を与える応力点（σφ,σθ）を主応力空間にプロットして等塑性仕事面を求めた．図2.3(b)は，(a)の応力の実験値を，当該のに対応する管軸方向単軸引張真応力で除して無次元化したものである．等塑性仕事面は応力比20:23～3:4方向に張り出した形状を有している．Yld2000による降伏曲面形状はこの傾向をよく捉えており，特に=0.002，0.01，0.025における等塑性仕事面とほぼ一致している．Hosfordによる降伏曲面と等塑性仕事面との一致の度合いは，の応力比1:1～3:4においてYld2000に比べてやや劣る．等塑性仕事面との最大誤差は，Hosfordの降伏曲面において7％，Yld2000の降伏曲面において4％であった．

(a)

(b)

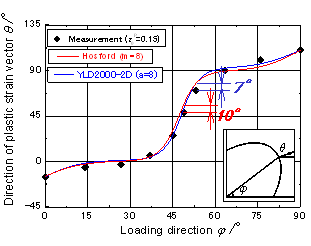
図3	5000系アルミニウム合金管の降伏曲面と各種理論降伏曲面との比較.(a)HosfordおよびYld200-2d降伏曲面との比較.(b)von Mises，Hillの2次および次数8のHosfordの降伏曲面との比較.

　さらに，塑性力学における基礎原理として，「材料に発生する塑性ひずみ増分は，当該の応力状態に対応する降伏曲面上の点において，その外向き法線ベクトル方向を向く」（法線則）がある．その原理の妥当性を検証した結果を図４に示す．ここで，応力比は応力経路の方向で表現している（管軸方向単軸引張りが，等二軸引張りが，円周方向単軸引張りが）．Yld2000による計算値は毎に異なるため，代表値として＝0.15における計算値を示している．HosfordおよびYld2000による計算値の差は小さく，どちらも実験値の傾向をおおよそ再現できている．実験値との誤差は，Hosfordの降伏条件式において最大で10°，Yld2000降伏条件式において最大で7° であり，これらの降伏関数を用いることにより，本円管材の塑性変形特性が実用上十分な精度で予測可能であることがわかる．

図4　塑性ひずみ増分の発生方向の測定結果とHosfordおよびYld200-2d降伏関数による計算値との比較

　このように，本試験機を用いることにより，実用金属円管材の弾塑性変形特性を高精度に測定することができ，ひいては最適な材料モデルの同定に効果を発揮する．
　今後も，自動車に代表される輸送機器や電子機器の軽量化に向けて，さまざまな金属管材が開発されるであろう．それら材料の弾塑性変形挙動の精密測定と異方性降伏関数を用いた材料モデリングの基礎研究は，研究内容そのものがサイエンスとして非常に魅力的なテーマである．さらに，実用的観点としては，高精度な成形シミュレーション技術を確立し，日本のもの作り技術の洗練度を維持・高度化する上で必要不可欠な研究であると確信している．

　参考文献

1)	桑原利彦・成原浩二・吉田健吾・高橋進，軸力と内圧を受ける5000系アルミニウム合金管の塑性変形特性の測定と解析，塑性と加工，44-506(2003), 281-286．
2)	. Kuwabara, M. Ishiki, M. Kuroda, S. Takahashi, Yield Locusand Work-Hardening Behavior of a Thin-Walled Steel Tube Subjected to Combined Tension-Internal Pressure, Journal de Physique IV, 105 (2003), 347-354.
3)	T. Kuwabara1, K. Yoshida1, K. Narihara1, S. Takahashi, Anisotropic plastic deformation of extruded aluminum alloy tube under axial forces and internal pressure, Int. J. Plasticity, 21-1(2005), pp 101-117