| マイクロ転造による動圧軸受の高精度加工 | |||||||
| 研究の背景・目的 | |||||||
| 金属のプレス加工は,安価な部品を大量に生産できるため,自動車用部材の加工などに適用されている.図1のように,プレス加工時に材料が破断する場合があり,これが試作期間およびコストの増大の原因となっている.そのため,金属材料の破断現象の解明,および成形限界の予測は,塑性加工の分野における重要な技術課題となっている. 成形限界の予測方法として,板厚ひずみまたは相当ひずみがある臨界値に達したときとする方法がある.これらは簡単な条件であり実用的であるが,実際には金属の破断は上記のような条件で律則されない.また,その他の方法として,比例負荷での成形限界ひずみをひずみ空間にプロットした成形限界線を用いる方法もある.成形限界線を図2中に黒線で示す.この曲線と破線で囲まれた領域が,破断することなく成形できる範囲となる.成形限界線は変形限界を把握しやすいので頻繁に用いられているが,成形限界線は材料が受けたひずみ経路に依存して変化する,という欠点を有する.その例を図2に示す.図中の赤線は予ひずみ(赤丸)を負荷した後,材料が破断するまで比例負荷を与えたときの成形限界線である.成形可能領域は明らかに変化している.つまり,この方法を実際の加工に適用する場合は,実際に材料が受けるひずみ経路に対応した成形限界線が必要となる.しかし,実際の加工で発生するひずみ経路は無数であり,それらをすべて同定することは不可能に近い. 以上のように材料の破断を正確に判定する手法は未だ確立されていない.生産現場では,精度がよく,簡便な成形性評価手法の開発が望まれている. |
 図1 プレス加工における破断 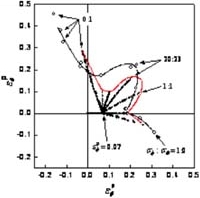 図2 成形限界線図(複合負荷Ⅰ) |
||||||
| 研究方法と特徴 | |||||||
| 当研究室では,成形限界を応力空間で表示した成形限界応力線に基づいた破断予測手法を提案している.この方法では,材料の応力状態が応力空間上に描かれた単一の破断限界曲線に達したとき材料が破断する,と判定する.この限界曲線は,応力およびひずみ経路には依存しないことを確認しており,上記のひずみ空間上の成形限界線よりも簡便な手法といえる.現在,応力を基準とした成形限界の評価方法について,実験的および理論解析の観点から研究を進めている. | 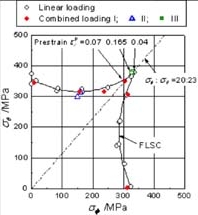 図3 成形限界応力線 |
||||||
| 研究成果 | |||||||
| 板材の成形限界実験において,破断時の応力を測定することは,極めて困難である.当研究室では,軸力-内圧型の2軸応力試験機を開発し2),円管材料を用いることにより,さまざまな応力経路・ひずみ経路下における成形限界応力の実測に成功し,応力による成形限界の判定方法の有効性を立証した.図3に各種ひずみ経路における成形限界線図を示す.ひずみ空間における成形限界線は明らかにひずみ経路に依存している. 次に,図2および図3のひずみ経路において,成形限界に達した瞬間の応力値を応力空間上にプロットした.その結果を図4に示す. 各成形限界応力はほぼ1つの曲線付近に集中している.つまり,応力で評価すれば,成形限界応力にはひずみ経路依存性がないということがわかった3). 一方,理論解析においては,Marciniak-Kuczynskiモデルに基づいた解析ソフトを開発した.精密な塑性不安定解析を行うには,高精度な構成則が不可欠である.そこで,本ソフトは,von Mises, Hill’48, Barlat-Lian, Yld2000-2dの4種類の降伏関数,および,関連流れ則,J2変形論,Kuroda-Tvergaardの非法線則モデルが組み込まれている.成形限界線および成形限界応力線の解析結果を図5に示す.本解析においても,成形限界線にひずみ経路依存性があっても,それを応力空間で表示するとひずみ経路依存性が消失することが明らかとなった.また,板材の破断予測方法として著名なStoren-Riceの分岐条件から成形限界応力がひずみ経路に依存しないことを示すこともできる. |
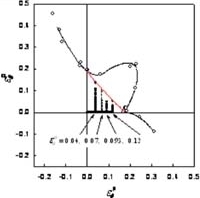 (a)複合負荷Ⅱ 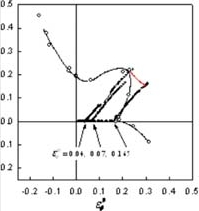 (b)複合負荷Ⅲ 図4 成形限界線図 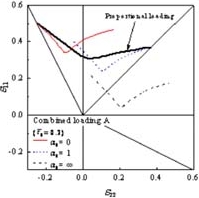 (a)成形限界線 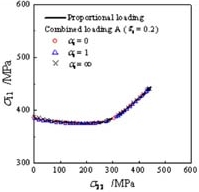 (b)成形限界応力線図 図5 Marciniak-Kuczynskiモデルによる成形限界解析の結果(:第1負荷の応力比(αI)) |
||||||
| 参考文献 | |||||||
|
|||||||