DPマッチング
2002/07/25 Acky(HTML 化 hazumi)
1.導入
| 某社長 | :僕がやって君がやらないわけないよなぁ. |
| 私 | :へ?何の話ですか? |
| 某社長 | :7月の担当は君にしようと思うんだよ. |
| 私 | :でも8月頭にある学会の準備が… |
| 某社長 | :期限までに終わらなかったら次の呑み会は倍払いだからね. |
| 私 | :勘弁してくださ〜い. |
そんなこんなで,「年長者から持ち回り」という至極尤もらしい理由によって第2回の担当となった私Ackyは,
パターン認識に関する研究を専門にしております.
パターンというのは,音声認識における音声,画像認識における画像,要は認識対象となる事象ですね.
これを認識するために,たとえば人の顔認識ならば,輪郭,目鼻立ち,唇の大きさといった特徴を抽出し,
それが基準を満たすか否かを調べます.
でも,CGやゲームを制作するのと違って,認識のプログラムって具体的に何をしたらいいのか,そのあたりの取っ付きが悪いんですよね.ある顔写真がAさんのかBさんのか調べたい場合なら,Aさんの顔写真とBさんの顔写真をそれぞれ持ってきて,さっきの写真がどっちに似てるかを調べればいい,という風に漠然とは想像できるんだけど,じゃあ「似てる」ってコンピュータにどうやって判断させたらいいんだろう...と悩んでしまう.
ところで,顔写真の例のように,認識対象となるパターンが何に似ているか,というアプローチで処理を行う手法は,パターンマッチングを用いた認識手法と呼ばれます.この手法では,認識結果の候補(先の例ならAさんとBさん)について,認識対象と比較可能なパターン(先の例ならAさんとBさんの顔写真)を辞書として用意しておきます.認識を行うときには,対象となるパターンに一番似ているものを辞書から選んで,それが誰の顔写真かを調べればいいわけです.
2.「似てる」の数値化とパターンマッチング
さて,「似てる似てない」の話に戻ります.顔でも音声でも,重ね合わせて一致したら...と処理出来ればいいんですが,
実際にはいろんな要因でパターンは変動しますから,完全一致なんてことはまず期待できません.
ちなみに,パターン認識の世界では,この「似ている」という尺度を数値化したものを「類似度」と呼びます.
ともかく,パターンマッチングを用いた認識では,パターン間に多少の違いがあろうとも,
それらが似ているかどうかを数値化する必要があります.
話を簡単にするため,パターンを1次元の符号列としましょう.例えば2つのパターン:
P1 = {a,b,b,b,b,c,c},P2 = {a,a,b,c,c,c}
は,完全一致こそしませんが,まあ似たようなものです.違いというと部分的な伸縮ぐらい...ということで,
伸縮マッチングなんですよ.このマッチング手法は,パターン内の部分的な伸び縮みを考慮しながら,
それらの類似度を計算する手助けをしてくれます.
代表的な伸縮マッチング手法として「動的計画法(Dynamic Programming)によるマッチング手法(略称:DPマッチング)」が挙げられます.
動的計画法ってのは,郵便や荷物の配達をどのような経路で行うか,といった問題を数学的に解決するアプローチの一種で,
最適な経路を求めることができる...って,まだ寝ちゃだめですよ.本当に眠いのはこれからです.
3.マッチングと類似度計算
「なんで似てる似てないの問題が最適経路と関係あるのか?」
なんか取っ付きの悪い問題を更に取っ付き悪くしてる気もしますね.まあ,文句は言わないで,とりあえず下の図でも見てくださいな.
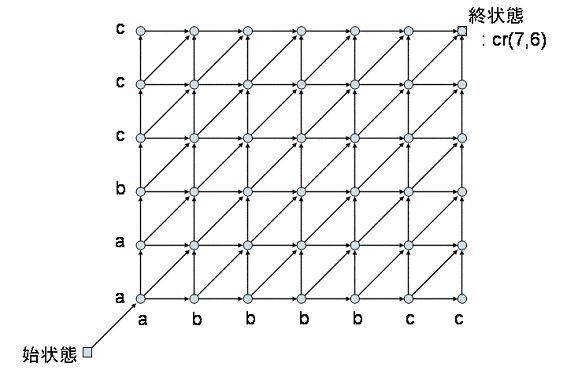
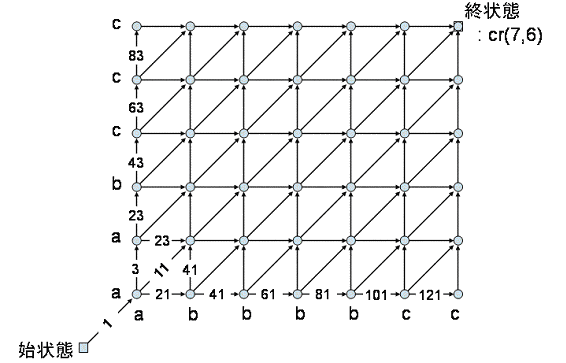
これは,横方向にP1,縦方向にP2を,それぞれ左下から並べて,
それで出来た平面に縦横斜めの矢印を付けただけの図です(始状態は実装の都合で付けた点ですので,今は気にしないでください).
この平面内で最適経路を求めるから,動的計画法なんですね.ちなみに,矢印は一方通行です.
では,パターンマッチングの話は暫し忘れて,始状態から終状態までの最適経路を求めることにします.
最適経路の条件は,距離が最小となることとします.各矢印の距離は図に示す通りです.

但し,交差点の下,及び左にある符号が異なる場合,その交差点に入る矢印の距離はペナルティとして10倍されます.
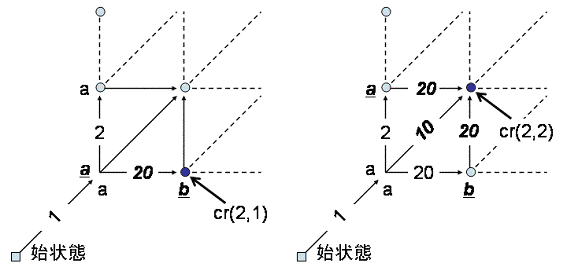
例えば,左から2番目,下から1番目の交差点:cr(2,1)では,下の符号がP1の2番目の符号:b,
左の符号がP2の1番目の符号:aになるので,左から入ってくる矢印の距離は2→20となります.
また,左から2番目,下から2番目の交差点:cr(2,2)では,下がP1の2番目:b,左がP2の2番目:aなので,
そこに入る3本の矢印全ての距離が10倍されます.
では,距離が最小になる経路(矢印列?)を求めてください...どうでしょう.たぶん,次の様になると思います.
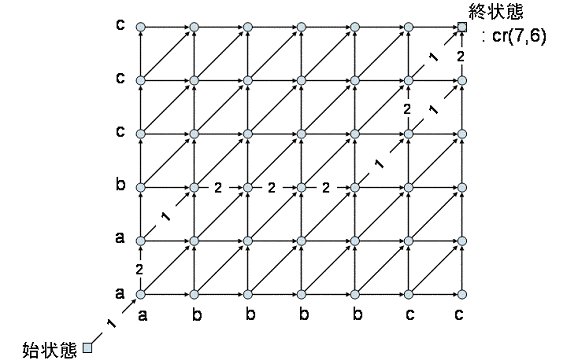
終状態の手前で2種類の経路が存在しますが,どっちでもいいです.このとき,距離の総和は14となるはずです.
以下にプログラミング可能な解法を示します.
まず,始状態から交差点cr(1,1)までの距離を求めますが,ここではP1もP2も符号がaとなるため,距離は1です.
次に,cr(2,1)とcr(1,2)についてですが,cr(1,1)からの距離はそれぞれ20と2ですから,
始状態からの距離はそれぞれ21と3になります.同様にcr(3,1)〜cr(7,1),cr(1,3)〜cr(1,6)について,
始状態からの距離は以下のようになります.
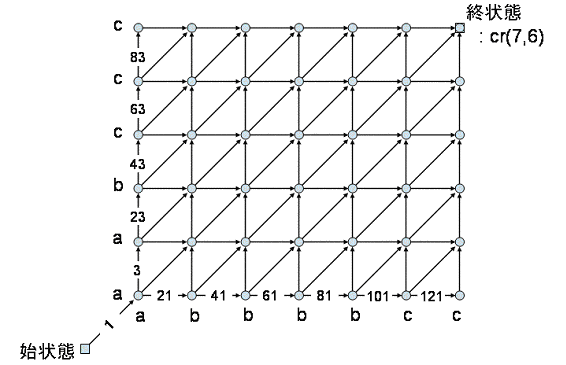
では,次にcr(2,2)について始状態からの距離を求めてみましょう.始状態からcr(2,2)までの経路には,
始状態→cr(1,1)→cr(2,1)→cr(2,2)
始状態→cr(1,1)→cr(2,2)
始状態→cr(1,1)→cr(1,2)→cr(2,2)
の3種類があります.ここで,cr(2,2)の直前の交差点となるcr(2,1),cr(1,1),cr(1,2)については,既に始状態からの距離が求まっていますので,これらをdist(2,1),dist(1,1),dist(1,2)とすると,cr(2,2)までの最短距離は,
dist(2,1) + l(cr(2,1)→cr(2,2))
dist(1,1) + l(cr(1,1)→cr(2,2))
dist(1,2) + l(cr(1,2)→cr(2,2))
の最小値となります.但しl(x→y)は,交差点x→交差点yまでの距離とします.それぞれ計算すると,
dist(2,1) + l(cr(2,1)→cr(2,2)) = 21 + 2 * 10 = 41
dist(1,1) + l(cr(1,1)→cr(2,2)) = 1 + 1 * 10 = 11
dist(1,2) + l(cr(1,2)→cr(2.2)) = 3 + 2 * 10 = 23
となり,最小距離は11であることがわかります.このとき,cr(2,2)に対して,直前の点がcr(1,1)であると記録しておきましょう.
このcr(2,2)を含めて,cr(i,j) (但し2<=i<=7,2<=j<=6)については,始状態からの距離が
dist(i,j-1) + l(cr(i,j-1)→cr(i,j))
dist(i-1,j-1) + l(cr(i-1,j-1)→cr(i,j))
dist(i-1,j) + l(cr(i-1,j)→cr(i,j))
の最小値となります.既にdist(1,1),dist(2,1)〜dist(7,1),及びdist(1,2)〜dist(1,6)は求まっていますから,
後は芋蔓式ですね.cr(2,2)のときと同様に,距離最小となる直前の交差点は記録しておきましょう.
これで最適経路を通った際の距離はd(7,6):終状態に記録されることになります.また,先に記録した直前の点を,
終状態からバックトレースする(逆に辿る)ことで,最適経路を導き出すことが出来ます.全ての矢印について累積の計算を行った結果は以下のようになります.

では,頭をパターンマッチングに戻してください.ここで導いた最短距離と最適経路は,それぞれP1とP2の間の距離,及びP1,P2に含まれる符号の対応付けを表しています.距離とは,パターン間の違いを表す概念で,これが小さいほどパターン間の類似度は大きくなります.実際,符号が異なる場合のペナルティは,似ていないパターン同士の距離を大きくしています.つまり,矢印毎の距離,及び符号が異なる場合のペナルティを調整すれば,DPマッチングによって類似度は計算できるということです.一方,最適経路から導き出される符号同士の対応付けは以下のようになります.
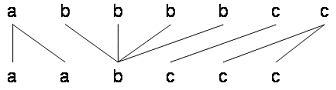
または,
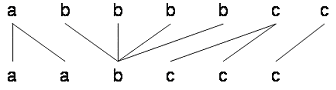
この対応付けから,伸縮マッチングがパターンの部分的な伸縮をうまく吸収していることがわかります.
4,終わりに
DPマッチングは,設計のシンプルさ故に制限もありますが,汎用性は高く多くのパターン認識で利用され,
同時に高い精度も実現しています.
まあ,他にもパターン認識の手法って色々あるんですけどね.その辺のお話は,また機会がありましたら.それでは.









