第5回

プログラミングおよび演習ＮＯ．5

Last-Modified: 2016.6.2

制御文には、①選択処理と②反復処理の2種類があり、このうち前回は①のif文を習いました。今週は、②の反復処理を行う制御文としてfor文を取り上げます。for文は特定の処理を何回も繰り返し実行したい場合に使います。if文とfor文は、使い方を知らないと満足なプログラムは作れないというぐらいに重要ですので、しっかり覚えるようにしてください。

　for文

for文の構造は以下のようになっています。

　　for(式1; 式2; 式3){

　　　　文1;
　　　　文2;
　　　　…
　　}

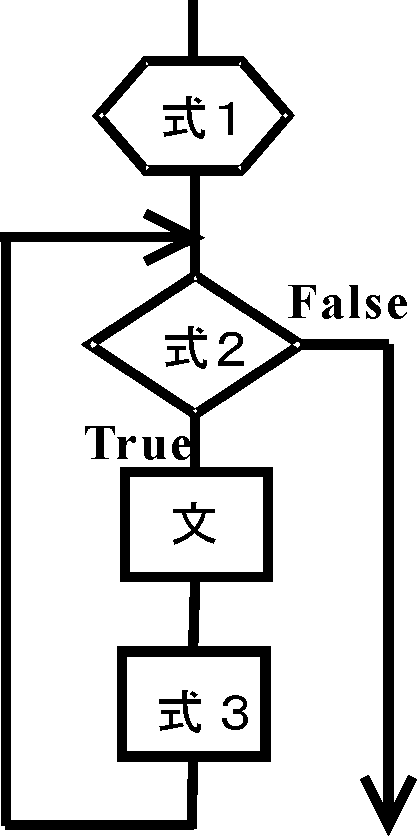
for文は、(式1; 式2; 式3)の条件に応じて、{…}の中の実行文を繰り返し実行します。ここで、(式1; 式2; 式3)の条件式は、フローチャートに示すように

　　式1：反復処理に用いるループ変数の初期値を与える。
　　式２：ループの最初で式２の条件が成立しているかどうかを調べる。
　　　成立していれば｛　｝の中の処理を繰り返す。成立していなければ処理を終了する。
　　式３：ループの最後に、式３を実行する。

という約束を意味します。

例えば、整数型のループ変数ｉを用いて、iを１からｎまで１ずづ増やしながら｛　｝の中の反復処理をｎ回繰り返すfor文は次のようになります。

　　for(i=1; i<=n; i++){
　　　　文１;
　　　　文２;
　　　　‥‥
　　}

この場合、①まず式１の部分でループ変数ｉの初期値をｉ=1に設定しています。次に、②式２の部分で、iがn以下であるかどうかを判断しています。iがｎ以下の場合は、そのまま｛　｝の中の実行文を実行します。そうでない場合は反復処理を終了します。 ③前者の場合、反復処理の最後にi++を実行し（iを一つ増やす。［注］を参照）①に戻る、という処理を繰り返します。この反復処理は、i=n+1になって式２の条件が成立しなくなった時に終了します。その結果、{文;}の中の反復処理が、i=1～nまでのn回繰り返し実行されることになります。

[注]：i++はインクリメント演算子で、i=i+1をあらわします（i+=1と書くことも出来ます）。同様に、i--はデクリメント演算子で、i=i-1を表します。iを２つづつ増やす場合は、i+=2(または、i=i+2)のように書きます。

++i, --iのように変数の前に、演算子を付ける書き方もあります。各々は

　　++ｉ　：　i=i+1の計算を行った後にiを使う
　　ｉ++　：　iを使ったあとにi=i+1の計算を行なう。

の違いがあります。for文の中で使った場合は、どちらを使っても構いません。

例5-1 は、for文を使った１からｎまでの数の和を求めるためのプログラムです。

例 5-1

#include<stdio.h>

int main(void)
{
    int sum,i,n;

    printf("Input a positive number ?\n");
    fflush(0);
    scanf("%d",&n);

    sum=0;
    for(i=1;i<=n;i++)
        sum=sum+i;

    printf("\nsum=%d\n",sum);

    return(0);
}

説明：
１からｎまでの数の和Ｓ_nは、

　　　　　(1+n)n
　　Ｓ_n＝　　　　.
　　　　　　　2

の公式を用いても計算できますが、上記のプログラムでは公式を用いずに、

　　Ｓ_n＝１＋２＋‥‥＋ｎ

を数値的に計算しています。このために、最初にsum=0 (S₀=0)を入れておいて、

　　１回目の繰り返し計算：　sum=sum+1　(S₁=S₀+1)
　　２回目の繰り返し計算：　sum=sum+2　(S₂=S₁+2)
　　　　　　　　‥‥
　　ｎ回目の繰り返し計算：　sum=sum+n　(S_n=S_n-1+n)

に従って計算を行っています。

演習問題 5-1 (Revised : 2016/06/02)

for文を使って以下の数列の和を計算するプログラムを作成してください。
　　　　　　　　　　　　　　　　　　　n
　S_n = 1^k+2^k+3^k+4^k+5^k+...+n^k = Σi^k
　　　　　　　　　　　　　　　　　　　i=1
ただし、nとkの値はキーボードから入力するようにする。nとして、正の数を入力した場合は計算を実行し、負の数を入力した場合は入力のやり直しを促す文章を出力した上で、何もせずにプログラムを終了させる。
実験では、kの値はk=1,2,3の3通り、nの値はkの値ごとに2通り以上について試すこととし、一つは10000以上のnを入力してください。考察では、真値（以下の公式を用いた手計算の結果）と比較して誤差がある場合にはその理由について考察し、さらにプログラムの動作について説明してください。

[補足]　手計算用の公式（注：プログラムには以下の公式を用いないこと）

　　k=1　 S_n=n(n+1)/2
　　k=2 　S_n= n(n+1)(2n+1)/6
　　k=3 　S_n=n²(n+1)²/4

for文を使うときの注意：　
■ループ変数は整数型を使う
例えば、

　　s=0.1+0.2+0.3+‥‥2.0

のように、0.1きざみで、0.1～2.0まで足し算する計算を考えます。
これを、double型のループ変数xを用いて

　　double s,x;
　　s=0.0;
　　for(x=0.1; x<=2.0;x+=0.1)
　　　　s=s+x;
　　printf("s=%le\n",s);

のようにすると、正しい値（21.0）が得られません。
このため、浮動小数点の演算結果を条件判定に使うことを避けて

　　int i;
　　double s,x;
　　s=0.0;
　　for(i=1; i<=20; i++)
　　　　s=s+i*0.1;
　　printf("s=%le\n",s);

のように整数型変数をループ変数に用います。すなわち、ループ変数には整数型の変数を使うようにしたほうが良いことになります。

演習問題５-２ (Revised : 2013/06/07)

①上記２つのプログラムの動作を確認してください。また、最初のプログラムでは正しく計算されない理由をその根拠と共に示してください。

ヒント：
for文の中に xおよびs の値を表示するためのprintf文を挿入して、繰り返すたびにこれらの値がどのように変化するか確認する。その上で、for文の繰り返し計算が、実際の計算で何回行われているか？繰り返しの終了判定が正しく行われているか？、などを調べてみよ。

②関連した問題として、int型のループ変数をfor文に用いて、double型の数0.1を1,000,000,000 回足す計算を行ってください。その一方で、1.0を 100,000,000 回足した結果はどうなりますか？結果を示した後で前者の計算誤差が大きくなる理由について説明してください。

ヒント：printf文の書式指定に%lf（あるいは%23.16le) などを用いて、16桁程度の桁数で表示する。少ない桁数で表示すると両者が同じ数であるかのように表示されることに注意する。

③余力のある人へ：double型の変数xをループ変数に使った上記①の最初のプログラムを、以下のヒントを参考に、正しい計算結果を出力するプログラムに作り変えてください。

ヒント：
倍精度実数xの比較演算は、丸め誤差を考慮して以下のようにする必要がある。

　　if( x == a ) の代わりに、if( fabs(x-a) < fabs(a)*1.0e-15 )
　　if( x <= a ) の代わりに、if( x <= a+fabs(a)*1.0e-15 )
　　if( x >= a ) の代わりに、if( x >= a-fabs(a)*1.0e-15 )

多重ループ：
for文を二重、三重に重ねて次のように書くことができます（for文に限らず、ある制御文の中に、別の制御文を次々と重ねていくことができます）。

　　　for(‥‥)｛
　　　　　‥‥
　　　　　for(‥‥)｛
　　　　　　　‥‥
　　　　　　　for(‥‥)｛
　　　　　　　　　‥‥
　　　　　　　}
　　　　　}
　　　}

[注意]　各々のループの始まりと終わりを分かりやすくするために、上記リストのように、ループが深くなる度ごとに、字下げ（インデント、indentation）を行います。for文にかぎらず、始まりの｛と終わりの｝の間は、必ず先頭に4文字程度の空白（またはTAB）をいれる（字下げする）習慣を身につけてください。

多重ループの使用例として、例えば、

　　int i,j,n;
　　double x;

　　n=10;
　　for(i=0; i<n; i++){
　　　　for(j=0; j<n; j++){
　　　　　　x= i*n+j;
　　　　　　printf("%4.0lf",x);
　　　　}
　　　　printf("\n");
　　}

のプログラムを実行すると結果はどうなりますか？。

演習問題５-３ (Revised : 2015/06/11)

出力が下記のようになるようにプログラムを作り変えてください。for文のループが深くなる度に、適正な字下げを施した、プログラムにしてください。また、プログラムの動作と出力結果を関連づけて説明して下さい。

   31   32   33   34   35   36   37   38   39   40
   41   42   43   44   45   46   47   48   49   50
   51   52   53   54   55   56   57   58   59   60
   61   62   63   64   65   66   67   68   69   70
   71   72   73   74   75   76   77   78   79   80
   81   82   83   84   85   86   87   88   89   90
   91   92   93   94   95   96   97   98   99  100
  101  102  103  104  105  106  107  108  109  110
  111  112  113  114  115  116  117  118  119  120
  121  122  123  124  125  126  127  128  129  130

発展問題：

出力が下記のようになるようにプログラムを作り変えてください。
ただし、３重ループにしてください。

   0    -1    -2    -3    -4    -5    -6    -7    -8    -9
 -10   -11   -12   -13   -14   -15   -16   -17   -18   -19
 -20   -21   -22   -23   -24   -25   -26   -27   -28   -29
 -30   -31   -32   -33   -34   -35   -36   -37   -38   -39
 -40   -41   -42   -43   -44   -45   -46   -47   -48   -49
 -50   -51   -52   -53   -54   -55   -56   -57   -58   -59
 -60   -61   -62   -63   -64   -65   -66   -67   -68   -69
 -70   -71   -72   -73   -74   -75   -76   -77   -78   -79
 -80   -81   -82   -83   -84   -85   -86   -87   -88   -89
 -90   -91   -92   -93   -94   -95   -96   -97   -98   -99

-100  -101  -102  -103  -104  -105  -106  -107  -108  -109
-110  -111  -112  -113  -114  -115  -116  -117  -118  -119
-120  -121  -122  -123  -124  -125  -126  -127  -128  -129
-130  -131  -132  -133  -134  -135  -136  -137  -138  -139
-140  -141  -142  -143  -144  -145  -146  -147  -148  -149
-150  -151  -152  -153  -154  -155  -156  -157  -158  -159
-160  -161  -162  -163  -164  -165  -166  -167  -168  -169
-170  -171  -172  -173  -174  -175  -176  -177  -178  -179
-180  -181  -182  -183  -184  -185  -186  -187  -188  -189
-190  -191  -192  -193  -194  -195  -196  -197  -198  -199

-200  -201  -202  -203  -204  -205  -206  -207  -208  -209
-210  -211  -212  -213  -214  -215  -216  -217  -218  -219
-220  -221  -222  -223  -224  -225  -226  -227  -228  -229
-230  -231  -232  -233  -234  -235  -236  -237  -238  -239
-240  -241  -242  -243  -244  -245  -246  -247  -248  -249
-250  -251  -252  -253  -254  -255  -256  -257  -258  -259
-260  -261  -262  -263  -264  -265  -266  -267  -268  -269
-270  -271  -272  -273  -274  -275  -276  -277  -278  -279
-280  -281  -282  -283  -284  -285  -286  -287  -288  -289
-290  -291  -292  -293  -294  -295  -296  -297  -298  -299

余力のある人は以下の問題にも挑戦してみてください。

演習問題5-4　指数関数

次式のテーラー展開式に従って、指数関数ｅ^xを計算するプログラムをつくってみてください。

　　ｅ^x= １＋ｘ＋ｘ²/2!＋ｘ³/3!＋…

（ヒント：何をforループのループ変数にすれば良いですか？）

また、x=1の場合について、nの値が1から20までのそれぞれの計算結果と真値e=2.718281828459045...とを比較して下さい。

発展問題：

ｘ=-5.5の場合について、真値ｅ^-5.5＝0.00408677…と結果を比較してみてください。この場合は、
　　　１　　　　　　　　　　　　　１
ｅ^x＝　　＝　　　　　　　　　　　　　　　　　.
　　　ｅ^-x　　　１＋(-x)＋(-x)²/2!＋(-x)³/3!＋…

の計算式を使ったほうが計算誤差が小さくできます。最初の計算式で誤差が大きくなるのは何故ですか？。