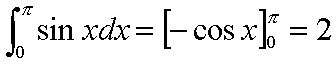
椺:僉乕儃乕僪偐傜乽1仺0仺0仺1仺1乿偲擖椡偡傞偲丄擇恑悢10011偼丄廫恑悢偱偼
栤1
int power(int n)偼丄1偮偺惍悢n(亞1)傪擖椡偡傞偲丄2偺傋偒忔
栤2
main()拞偵偍偄偰丄5寘栚偐傜弴斣偵1寘栚傑偱丄僉乕儃乕僪偐傜0傑偨偼1偺惍悢傪撉傒崬傒傑偡丅曄悢n偑壗寘栚偐傪昞偡偲偟偰丄戣堄偵増偆傛偆[嬻棑4]傪杽傔側偝偄丅
栤3
僉乕儃乕僪偐傜擖椡偡傞惍悢抣傪丄曄悢a偵奿擺偟傑偡丅曄悢a偼0傑偨偼1偱側偗傟偽側傝傑偣傫(擇恑悢)丅惓偟偄抣偑擖椡偝傟偨応崌偼墘嶼傪幚峴丄乽0傑偨偼1乿埲奜偺抣偑撉傒崬傑傟偨応崌偼丄乽惓偟偄抣傪擖椡偣傛乿偲夋柺偵昞帵偟傑偡丅戣堄偵増偆傛偆[嬻棑5],[嬻棑6]傪杽傔側偝偄丅
栤4
娭悢int power(int n)傪屇傃弌偟丄壗寘栚偐傪昞偡曄悢n偺抣傪堷偒搉偟傑偡(幚堷悢)丅娭悢power()偺曉傝抣(栠傝抣)2n-1傪曄悢ans偵戙擖偟傑偡丅戣堄偵増偆傛偆[嬻棑7]傪杽傔側偝偄丅
栤5
曄悢sum偵曄悢ans偺抣傪壛偊丄怴偨側sum偺抣偲偟傑偡丅戣堄偵増偆傛偆[嬻棑8]傪杽傔側偝偄丅
(僾儘僌儔儉撪嵍抂偺峴斣崋偼曋媂忋晅偗偨偵偡偓傑偣傫丅戞2栤傕摨條)
1:#include <stdio.h> /* 擇恑悢傪廫恑悢傊偲曄姺偡傞 */
2:int power(int n) /* 2偺傋偒忔2(n-1)寁嶼梡娭悢 */
3:{
4: int i,ans;
5: ans=1;
6: if([嬻棑1]){
7: for([嬻棑2]){
8: [嬻棑3] /* 2偺傋偒忔寁嶼 */
9: }
10: }
11: return ans;
12:}
13:int main() /* main */
14:{
15: int n,a,ans,sum;
16: sum=0;
17: n=5; /* 擖椡抣偼5寘栚偐傜僗僞乕僩 */
18: while([嬻棑4]){ /* 5寘栚偐傜1寘栚傑偱while儖乕僾 */
19: printf("2恑悢(0傑偨偼1)傪擖椡\n");
20: [嬻棑5] /* 僉乕儃乕僪偐傜曄悢a傊擖椡 */
21: if([嬻棑6]){
22: printf("%d寘栚:%d\n",n,a);
23: if(a==1){ /* a偑1偺応崌 */
24: ans=[嬻棑7]
25: [嬻棑8]
26: }
27: n--;
28: }
29: else{
30: printf("惓偟偄抣傪擖椡偣傛\n");
31: }
32: }
33: printf("擖椡抣傪廫恑悢偱昞偡:%d\n",sum);
34: return 0;
35:}
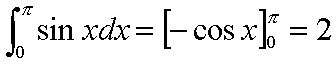
栤1
杮僾儘僌儔儉拞偵偍偄偰悢妛儔僀僽儔儕乕傪棙梡偟傑偡丅戣堄偵増偆傛偆 [嬻棑1]偵昁梫側僿僢僟乕僼傽僀儖柤傪彂偒側偝偄丅
栤2
嬫暘媮愊朄(屻弎偡傞乽嶲峫乿嶲徠偺偙偲)傪棙梡偡傞偨傔丄愊暘嬫娫0亝x亝兾傪曄悢N傪梡偄偰N摍暘偟丄曄悢dx=兾/N偲偟傑偡(摍暘悢N)丅戣堄偵増偆傛偆[嬻棑2]傪杽傔側偝偄丅側偍丄墌廃棪兾偺抣傪昞偡偺偵丄杮僾儘僌儔儉拞偱愝掕偟偨儅僋儘pi丄傕偟偔偼丄儅僋儘M_PI(gcc僐儞僷僀儔偵偍偄偰偁傜偐偠傔愝掕偝傟偰偄傞儅僋儘偺堦偮)傪棙梡偟偰傛偄丅
栤3
for儖乕僾撪偵偰曄悢k偺抣傪0偐傜N-1傑偱堦偮偯偮憹壛偝偣丄嬫暘媮愊朄偵傛傝丄
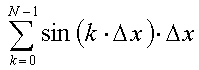
栤4
僼傽僀儖kekka.dat傪彂偒崬傒儌乕僪偱奐偒傑偡丅戣堄偵増偆傛偆[嬻棑5]傪杽傔側偝偄丅
栤5
夝愅抣2丄摍暘悢偺抣N丄嬫暘媮愊朄偵傛傞寁嶼抣sum傪丄夋柺偵昞帵丄摨條偵丄僼傽僀儖kekka.dat傊偲彂偒弌偟傑偡丅戣堄偵増偆傛偆[嬻棑6]傪杽傔側偝偄丅
栤6
摍暘悢偺抣偲偟偰N=10,N=100偲2捠傝愝掕偟偨応崌偺寁嶼抣sum傪丄夝摎棑偵偦傟偧傟彂偒側偝偄丅
1:#include<stdio.h> /* 嬫暘媮愊朄 */
2:#include<stdlib.h>
3:#include<[嬻棑1]> /* 悢妛儔僀僽儔儕乕棙梡 */
4:#define pi 3.1415926 /* 墌廃棪兾偺抣偲偟偰儅僋儘pi傪愝掕 */
5:int main()
6:{
7: FILE *fp; /* 僼傽僀儖億僀儞僞 */
8: int N,k;
9: double dx,sum;
10: N=10; /* 愊暘嬫娫傪N摍暘丄N偺抣偼10偲偡傞 */
11: dx=[嬻棑2] /* 儮x偺抣愝掕 */
12: sum=0; /* 寁嶼偝傟偨愊暘抣傪奿擺偡傞曄悢sum */
13: for([嬻棑3]){
14: [嬻棑4] /* 嚁sin(k丒儮x)丒儮x傪寁嶼 */
15: }
16: fp=[嬻棑5] /* 僼傽僀儖kekka.dat僆乕僾儞 */
17: if(fp==NULL){
18: printf("Can not open kekka.dat!\n");
19: exit(1);
20: }
21: printf("夝愅抣=2,摍暘悢=%d,嬫暘媮愊抣=%lf\n",N,sum);
22: [嬻棑6] /* 僼傽僀儖kekka.dat傊弌椡 */
23: fclose(fp); /* 僼傽僀儖僋儘乕僘 */
24: return 0;
25:}
(嶲峫:娭悢f(x)傪a亝x亝b偺斖埻偱嬫暘媮愊偡傞応崌偼埲壓偺捠傝偵側傝傑偡丅愊暘嬫娫傪N摍暘偟丄儮x=(b-a)/N偲梌偊傑偡丅暘揰傪a,a+儮x,a+2丒儮x,丒丒丒,a+(N-1)丒儮x偲偟傑偡丅偦偺寢壥丄愊暘抣傪
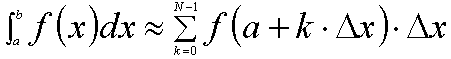
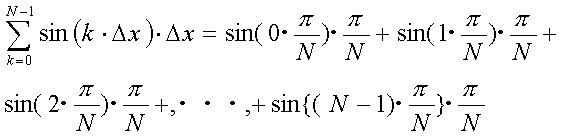
嬫暘媮愊朄偱偼丄榓偺斖埻傪0亝k亝N-1偱偼側偔丄1亝k亝N偲愝掕偟偨丄
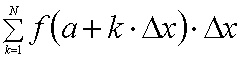
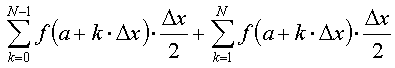
http://www.tuat.ac.jp/~kamelab/gcc/index.html 僐儞僺儏乕僞僾儘僌儔儈儞僌墘廗II 婽揷丒嵅摗僋儔僗偺儁乕僕傊