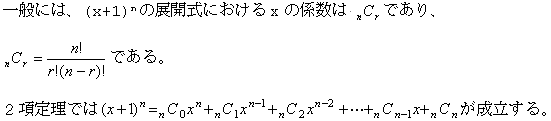
以下は、キーボードから正整数nを読みとり、階乗計算(n!=n×(n-1)×(n-2)×…×1)を実行、画面に結果を表示するプログラムの例です(左端の行番号は便宜上付けたにすぎません、以下同様)。

1:#include<stdio.h>  /* 階乗計算 */
2:void main(void){
3:	int n,i,a;
4:	printf("正整数をキーボードから入力して下さい\n");
5:	scanf([空欄1]);
6:	if([空欄2]){
7:		printf("正の数を入力して下さい。\n");
8:	}
9:	else{
10:		a=1;
11:		for(i=1; i<=n; i++){
12:			[空欄3]
13:		}
14:		printf("n!=%d",a);
15:	}
16:}

<解答>(1点)
"%d", &n

問2
正整数が入力されない場合、「正の数を入力して下さい。」と表示し、正数が入力された場合は階乗計算を行います。[空欄2]を埋めなさい。

<解答>(2点)
次の三つどれでも可。
解1: n<=0
解2: n<1
解3: n<0

問3
階乗計算の結果をaに代入します。[空欄3]を埋めなさい。

<解答>(2点)
次のどちらも可。
解1: a=a*i;
解2: a=a*(n-i+1);

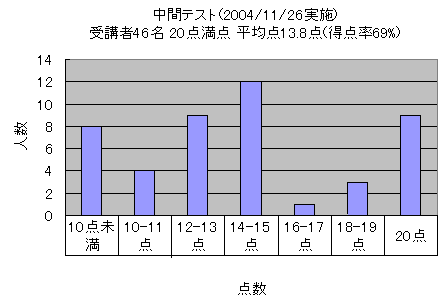
以下は、第1問の階乗計算プログラムを発展させ、キーボードから入力した正整数を元に二項係数を計算、画面上に表示するプログラムの例です。二項係数とは、(x+1)ⁿを展開した場合の各項の係数を表し、例えば、n=2と入力した場合、(x+1)×(x+1)=x²+2x+1なので、
1 2 1
と画面に表示します。
<ヒント>

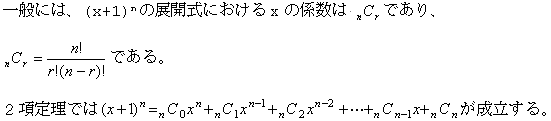
問1
_nC_rをr=0からr=nまで順に計算します。[空欄1]を埋めなさい。

<解答>(1点)
次のどちらも可。
解1: r=0; r<=n; r++
解2: r=n; r>=0; r--

問2
r!の結果をbに代入します。[空欄2]を埋めなさい。

<解答>(1点)
次のどちらも可。
解1: b=b*i;
解2: b=b*(r-i+1);

問3
(n-r)!の結果をcに代入します。[空欄3],[空欄4]を埋めなさい。

<解答>(2点。空欄1つにつき1点。但し空欄3が正解の場合のみ空欄4を採点対象とす。)
空欄3の結果によって大きく2つに分けられる。
解1:
空欄3: i=1; i<=n-r; i++ または i=n-r; i>=1; i--
空欄4: c=c*i; または c=c*(n-r-i+1);
解2:
空欄3: i=r; i<=n-1; i++ または i=n-1; i>=r; i--
空欄4: c=c*(n-i); または c=c*(i-r+1);

問4
二項係数_nC_rの値を変数dに代入します。[空欄5]を埋めなさい。

<解答>(1点)
次のどちらも可。
解1: d=a/(b*c);
解2: d=a/b/c;

1:#include <stdio.h> /*二項係数の計算*/
2:void main(void){
3:	int i,r,n,a,b,c,d;
4:	printf("正整数をキーボードから入力して下さい\n");
5:	scanf(/* 第1問 問1と同一 */);
6:	if(/* 第1問 問2と同一 */){
7:		printf("正の数を入力して下さい\n");
8:	}
9:	else{
10:		a=1;
11:		for(i=1; i<=n; i++){
12:			/* 第1問 問3と同一 */ /* n!を計算 */
13:		}
14:		for([空欄1]){
15:			b=1; 
16:			c=1;
17:			for(i=1; i <= r ; i++){
18:				[空欄2] /* r!を計算 */
19:			}
20:			for([空欄3]){
21:				[空欄4] /* (n-r)!を計算 */
22:			}
23:			[空欄5] /* nCrを計算 */
24:			printf("%d ",d); /* nCrを表示 */
25:		}
26:		printf("\n");
27:	}
28:}

平面上のベクトルA_n=(a_n,b_n)を考えます。ベクトルA₀の2成分(a₀,b₀)はキーボードから与えられ、次に示す漸化式により1≦n<10の各項が求まるものとします。

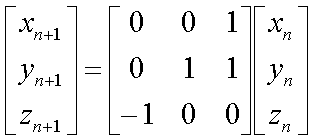
以下は、各A_n=(a_n,b_n)の値、及びA₀との内積(=A_n・A₀)を求め、結果をファイルに出力するプログラムの例です。

1:#include<stdio.h> /* 漸化式により生成される平面ベクトル */
2:#include<stdlib.h>
3:void main(void){
4:float a[10],b[10],p[10]; /* an:配列a,bn:配列b,内積:配列p */
5:int i;
6:char fname[20];
7:FILE *fp;
8:	printf("2数(a0,b0)を入力して下さい=>");
9:	[空欄1]
10:	for(i=0;i<9;i++){
11:		a[i+1]=b[i]*(-0.5);     /* 漸化式 an */
12:		[空欄2]		      /* 漸化式 bn */
13:	}
14:	for(i=0;i<10;i++){
15:		[空欄3]		      /* 内積計算 */
16:	}
17:	printf("ファイル名を入力してください=>");
18:	scanf("%s",fname);
19:	fp=fopen([空欄4]); /* ファイルオープン */
20:	if(fp == NULL){
21:		printf("%sをオープンできません\n",fname);
22:		exit(1); /* プログラム強制終了 */
23:	}
24:	for(i=0; i<10; i++){
25:		[空欄5] /* ベクトル成分、内積をファイルに書き出す */
26:	}
27:	fclose([空欄6]); /* ファイルクローズ */
28:}

問1
キーボードから2数a₀,b₀を読みとり、それぞれ配列a[0],b[0]へ代入します。[空欄1]を埋めなさい。

<解答>(1点)
次のどちらも可。また、%fが%eとなっていても、あるいは、"%f,%f"のようにコンマ(,)が記述されている解も可。
解1:
scanf("%f %f",&a[0],&b[0]);
解2:
scanf("%f",&a[0]);
scanf("%f",&b[0]);

問2
漸化式に沿ってb_n(1≦n<10)の値を求め、配列b[i](1≦i<10)に代入します。[空欄2]を埋めなさい。

<解答>(1点)
b[i+1]=a[i]*0.5;

問3
各A_n=(a_n,b_n)(0≦n<10)と A₀=(a₀,b₀)との内積(=A_n・A₀)を求め、p[i] (0≦i<10)に代入します。[空欄3]を埋めなさい。

<解答>(1点)
p[i]=a[i]*a[0]+b[i]*b[0];

問4
ファイルを「書き込みモード」で開きます。[空欄4]を埋めなさい。

<解答>(1点)
fname, "w"

問5
ベクトルの成分、内積をファイルに以下の形式にて書き出します。[空欄5]を埋めなさい。
ベクトルA0=(***.****,***.****),A0との内積=*****.****
ベクトルA1=(***.****,***.****),A0との内積=*****.****
・・・
ベクトルA9=(***.****,***.****),A0との内積=*****.****

<解答>(2点)
fprintf(fp,"ベクトルA%d=(%8.4f,%8.4f),A0との内積=%10.4f\n",i,a[i],b[i],p[i]);
\nはなくとも可とする。また、%7.4f等、小数点以下4桁表示が可能な記述であれば可、%fのみの場合1点減点。また、fprintfではなく、printfで記述した場合、
printf("ベクトルA%d=(%8.4f,%8.4f),A0との内積=%10.4f\n",i,a[i],b[i],p[i]);
であれば1点のみ与える。

問6
ファイルを閉じます。[空欄6]を埋めなさい。

<解答>(1点)
fp

問7
a₀=64.0,b₀=128.0として本プログラムを動かした場合に得られるベクトルA₅=(a₅,b₅),A₆=(a₆,b₆),A₇=(a₇,b₇)の各成分及びA₀との内積を求め、解答欄に記入しなさい。

<解答>(3点。A₅, A₆, A₇ 各成分及び内積がそれぞれ正解の場合にのみ、各1点ずつ。)
a₅=-4.0000 b₅=2.0000 内積A₅・A₀=0.0000
a₆=-1.0000 b₆=-2.0000 内積A₆・A₀=-320.0000
a₇=1.0000 b₇=-0.5000 内積A₇・A₀=0.0000
表示形式が、
a₅=-4 b₅=2 内積A₅・A₀=0
等、小数点以下4桁まで表示されていなくとも、数学的に正しい答であれば可。

<全体への注意点>
文の最後のセミコロン(;)抜けミス(例: 第1問 問3 a=a*iとした場合等)、また、forループかっこ内でのセミコロンを余分に付けるミス(例: 第2問 問1 r=0; r<=n; r++;とした場合等)については、正解部分について累計し、以下の基準に従い、総得点から減点する。
1-2個: 減点0点
3-5個: 減点1点
6個以上: 減点2点