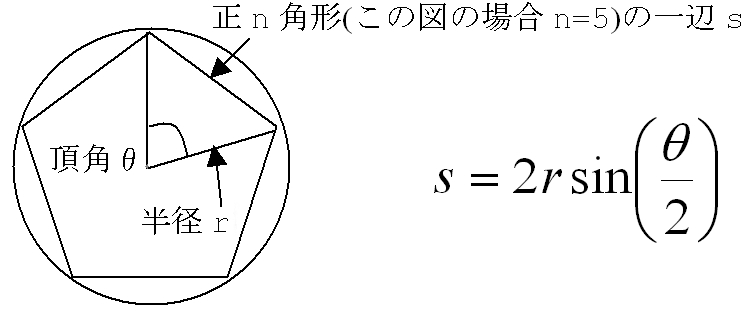
以下は、半径r(=100.0)の円に内接する正n角形(n≧3)の1辺の長さsを計算するプログラムの例です(左端の行番号は便宜上付けたにすぎません。第2問も同様)。
(参考)
円の半径をr、内接する正n角形(n≧3)の一辺の長さをs、一辺sを底辺とし、半径rとで作る二等辺三角形の頂角をθ(ラジアン単位の場合θ=2π/n、度数の場合θ=360゜/n)とすると、以下の関係式を満たす。

1: #include <stdio.h>
2: #include <[空欄1]>
3: #define pi 3.141592
4: double calc(double rr,int nn);
5: void main(void)
6: {
7: double r,s;
8: int n;
9: r=100.0;
10: printf("円(半径r=100.0)に内接する正多角形の辺の数n(n≧3)を代入\n");
11: scanf("%d",&n);
12: if([空欄2])
13: {
14: s=[空欄3]
15: printf("円の半径r:%lf\n",r);
16: printf("正%d角形の1辺の長さs:%lf\n",n,s);
17: }
18: else
19: {
20: printf("正しい値を入力して下さい\n");
21: }
22: }
23: double calc(double rr,int nn)
24: {
25: double theta,s;
26: theta=[空欄4]
27: s=[空欄5]
28: [空欄6]
29: }
問1
2行目、本プログラム中において数学関数sin()を使用するために、必要なヘッダーファイルの名称を[空欄1]へ書きなさい。
<解答>(1点)
解 math.h
問2
12行目、キーボードから入力された値nが、n≧3の場合にのみ正多角形の1辺の長さを計算し、それ以外の場合は、20行目で「正しい値を入力して下さい」と表示します。題意に沿うように[空欄2]を埋めなさい。
<解答>(1点)
解 n>=3
nが整数で定義されているので、n>2も正解である。
問3
14行目、変数r,nの値を関数calc()に引き渡し、計算結果を変数sに代入します。題意に沿うように[空欄3]を埋めなさい。
<解答>(2点)
解 calc(r,n);
関数calc()を使わず、main()関数内で直接sを求める場合(例:2*r*sin(pi/(double)n);)、問7の正解にはたどりつけるが、問題文の主旨から外れるので、1点減点。
問4
26行目、正多角形の1辺と円の半径とで為す二等辺三角形の頂角を変数thetaに代入します。題意に沿うように[空欄4]を埋めなさい。なお、変数thetaの単位は「ラジアン」または「度(゜)」どちらも可とします(πラジアン=180゜)。
<解答>(2点)
解 2.0*pi/(double)nn;
・マクロpiを使わず、2.0*3.141592/(double)nn;とした場合も正解とする。
・変数thetaの単位に「ラジアン」を使わず、「度(゜)」を使用した場合は360.0/(double)nn;が正解となる。
・マクロpiが倍精度実数であるため、以下のような記述例それぞれにおいて、可/不可となる。
可の例: 2*pi/nn等
不可の例: (2/n)*pi(nがint型(整数)でかつn≧3のため、本プログラムにおいて、2/nの演算結果は常にゼロとなってしまう)
・thetaの定義として、二等辺三角形の頂角の1/2を取った場合(pi/((double)nn);)は、問5の解との整合性が取れている場合に限り正解とする(問5の解参照)。
問5
27行目、正多角形の一辺の長さを計算し、変数sに代入します。題意に沿うように[空欄5]を埋めなさい。なお、問4において、変数のthetaの単位に「ラジアン」または「度 (゜)」を採用した場合との整合性を取ること。なお、関数sin()の引数(単位はラジアン)と返り値は以下の通り。
問6
28行目、計算結果sを関数calc()の返り値とします。題意に沿うように[空欄6]を埋めなさい。
<解答>(2点)
解 return s;
問7
n=36とした場合の本プログラムの計算結果を解答用紙の所定欄に書きなさい。
<解答>(2点)
解 17.431145
17.4や17.43115のように、桁を四捨五入したものも正解とする(但し、整数部分17のみを記述した場合は不可)。
以下は、cleos32上で5個の整数乱数を発生させ、int型配列a[5]の各成分(a[0],a[1],・・・,a[4])に代入し画面に表示、その和(a[0]+a[1]+・・・+a[4])を求めるプログラムの例です。
1: #include <stdio.h>
2: #include <stdlib.h>
3: #include <time.h>
4: void main(void)
5: {
6: int i, rn, n, num, a[5], sum1, sum2;
7: int [空欄1]
8: unsigned int seed;
9: int nowtime;
10: time([空欄2]);
11: seed=(unsigned int)nowtime;
12: srand([空欄3]);
13: for(i=0; i< 5 ; i++)
14: {
15: rn=rand();
16: a[i]=rn;
17: }
18: [空欄4]
19: sum1=0;
20: sum2=0;
21: for(i=0; i< 5 ; i++)
22: {
23: printf("配列a[%d]:%d\n",i,a[i]);
24: sum1+=a[i];
25: }
26: printf("配列の和sum1:%d\n",sum1);
27: for(i=0; i< 5 ; i++)
28: {
29: printf("配列a[%d](ポインタ利用):%d\n",i,*(a_ptr+i));
30: [空欄5]
31: }
32: printf("配列の和(ポインタ利用)sum2:%d\n",sum2);
33: }
問1
7行目、int型ポインタ変数a_ptrを宣言します。[空欄1]を埋めなさい。
<解答>(2点)
解 *a_ptr;
問2
10行目、関数time()へ、変数nowtimeのアドレスを渡します。 [空欄2]を埋めなさい。
<解答>(1点)
解 &nowtime
問3
12行目、乱数表の種を決める関数srand()の実引数として、本プログラム中で適切な変数を考え、[空欄3]を埋めなさい。
<解答>(1点)
解 seed
問4
18行目、ポインタ変数a_ptrに配列a[5]の基底アドレスの値を代入します。題意に沿うように[空欄4]を埋めなさい。
<解答>(2点)
解 a_ptr=a;
以下も正解となる。
a_ptr=&a[0];
a_ptr=&a;(&aは、配列の基底アドレスではなく、配列そのものへのアドレスを示す。値は基底アドレスと同一のため正解となる(詳しくは中間テスト(2005/12/02実施 2005/12/09返却)解答及び採点基準のページ 第2問 問1の別解参照のこと)。
問5
30行目、変数sum2に配列a[5]の各成分の値(a[0],a[1],・・・,a[4])を足し算、和を求めます。但し、ポインタ変数a_ptrを利用して記述すること。題意に沿うように[空欄5]を埋めなさい。
<解答>(2点)
解 sum2+=*(a_ptr+i);
・演算記号+=を使わず、sum=sum2+*(a_ptr+i);も正解。
・forループを利用せず、sum2=*(a_ptr);*(a_ptr+1);*(a_ptr+2);*(a_ptr+3);*(a_ptr+4);と、直接和を求める方法も、一応可とする(成分の数がもしも1000個だったら、この記述方法では一体どうするのであろうか?)。
<全体への注意点>
文の最後のセミコロン( ; )抜けミス(例: 第1問 問3 calc(r,n)とした場合)については、ミスがなければ正解となる箇所についてのみ累計し、以下の基準に従い総得点から減点する。
1-2個: 減点0点
3-5個: 減点1点
6個以上: 減点2点
