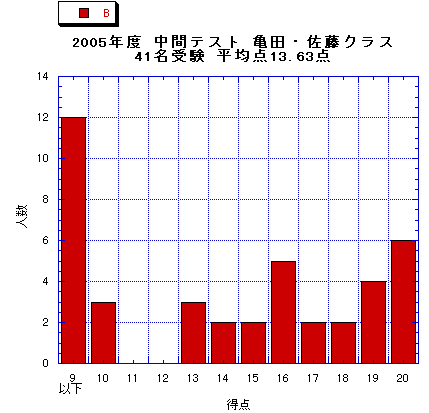
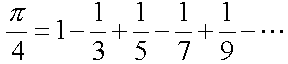 式(1)
式(1)
円周率πの近似値を、次に示す級数(注*)から求めるプログラムについて、以下の問いに答えなさい。
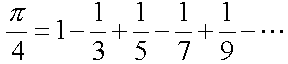 式(1)
式(1)(注*)「Leibnizの級数」と呼ばれ、奇数番目の項では1/(2n-1)の足し算、偶数番目の項では1/(2n-1)の引き算を、それぞれ行います。しかし、この級数は収束が遅いため、円周率の値を精密に計算する場合には、他の公式(例:Machinの公式)が利用されます。
(プログラム内左端の行番号は便宜上付けたにすぎません。以下同様)
1:#include<stdio.h> /*円周率の計算例*/
2:void main(void){
3: int n,nmax;
4: [空欄1]
5: sum=0.0;
6: nmax=100;
7: for([空欄2]){
8: if([空欄3]){
9: [空欄4]
10: }
11: else{
12: [空欄5]
13: }
14: }
15: pi=sum*4.0; /*円周率の計算値を変数piに格納*/
16: printf("円周率:%lf\n",pi);
17: }
問1
<解答>(2点)
解 double sum,pi;
倍精度ではなく単精度float sum,pi;とした場合、1点減点。また、piを、読み間違いもしくは書き間違いでp1とした場合も1点減点。
問2
本プログラムでは、n=1からn=nmaxに達するまで、nの値を1づつ増加させ、繰り返し計算を行います。題意に沿うように[空欄2]を埋めなさい。
<解答>(1点)
解 n=1;n<=nmax;n++
nmaxを使わずn<=100としても可。
問3
式(1)の級数和を変数sumに代入します。その際、項が奇数番目か偶数番目かによって、1/(2n-1)の値を足し算/引き算の区別をします。題意に沿うように[空欄3],[空欄4],[空欄5]を埋めなさい。
<解答>(空欄1つにつき1点 計3点)
[空欄4]、[空欄5]のどちらに奇数番目の項を入れるか偶数番目の項を入れるかにより、[空欄3]の解1種類について[空欄4,5]の解答は2つに分かれる。また、[空欄4,5]では、1/(2n-1)の項に対し倍精度実数計算を施す必要があることに注意せよ。このため、int型変数nをキャスト(double)するか、もしくは、倍精度実数を計算に含めなければならない(例: 1を1.0や(double)1とする)。
解1 [空欄3]: (n%2)!=0; [空欄4]: sum=sum+1.0/(double)(2*n-1); [空欄5]: sum=sum-1.0/(double)(2*n-1);
解2 [空欄3]: (n%2)==0; [空欄4]: sum=sum-1.0/(double)(2*n-1); [空欄5]: sum=sum+1.0/(double)(2*n-1);
空欄[3]の解として、(n%2)==1;、また、変数nがint型であることを利用した(n/2)==(n-1)/2も可。その場合以下の解となる。
解3 [空欄3]: (n%2)==1; [空欄4]: sum=sum+1.0/(double)(2*n-1); [空欄5]: sum=sum-1.0/(double)(2*n-1);
解4 [空欄3]: (n%2)!=1; [空欄4]: sum=sum-1.0/(double)(2*n-1); [空欄5]: sum=sum+1.0/(double)(2*n-1);
解5 [空欄3]: (n/2)==(n-1)/2; [空欄4]: sum=sum+1.0/(double)(2*n-1); [空欄5]: sum=sum-1.0/(double)(2*n-1);
解6 [空欄3]: (n/2)!=(n-1)2; [空欄4]: sum=sum-1.0/(double)(2*n-1); [空欄5]: sum=sum+1.0/(double)(2*n-1);
[空欄3]について。
n%2!=0;のように、カッコを省略しても可。
[空欄4,5]について。
sum=sum+1.0/(double)(2*n-1);をsum+=1.0/(double)(2*n-1);としても可(C言語における記述法)。sum=sum-・・・をsum-= ・・・とすることも同様の理由により可。
1/(2n-1)の計算時に倍精度実数であることが考慮されておれば可。
可の例: 1.0/(2*n-1), 1/(2.0*n-1), 1/(2*n-1.0), 1/(2*(double)n-1)等
不可の例: 1/(2*n-1)(nがint型のため今回のプログラムでは常にゼロとなってしまう), (double)(1/(2*n-1))(分数計算後にキャスト(double)を行っても、倍精度実数のゼロ(0.0)になるだけである)
問4
nmax=100,1000と設定した条件で本プログラムを用いて計算、画面に表示された円周率の値をそのまま解答欄に書きなさい。
<解答>(1つにつき1点 計2点)
nmax=100の場合 解 3.131593
nmax=1000の場合 解 3.140593
キーボードからベクトル(x0,y0,z0)の3成分を初期値として与え、以下に示す漸化式によってベクトル(xn,yn,zn)の各成分を順次求めます。
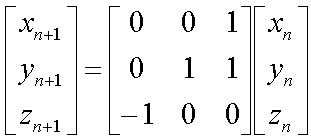 式(2)
式(2)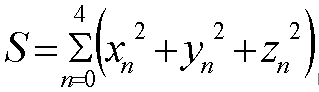 式(3)
式(3)
1: #include<stdio.h> /*二乗和の計算*/
2: #include<stdlib.h>
3: void main(void){
4: int x[10],y[10],z[10]; /*配列の要素をあらかじめ多めに定義*/
5: int n,s;
6: char fname[20];
7: FILE *fp;
8: [空欄1] /*x0,y0,z0の値をキーボードから入力*/
9: s=0;
10: for([空欄2]){
11: [空欄3] /*式(2)に従ってxを順次求める*/
12: [空欄4] /*式(2)に従ってyを順次求める*/
13: [空欄5] /*式(2)に従ってzを順次求める*/
14: [空欄6] /*式(3)に従ってSを求める*/
15: }
16: printf("X=(%d,%d,%d,%d,%d)\n",x[0],x[1],x[2],x[3],x[4]);
17: printf("Y=(%d,%d,%d,%d,%d)\n",y[0],y[1],y[2],y[3],y[4]);
18: printf("Z=(%d,%d,%d,%d,%d)\n",z[0],z[1],z[2],z[3],z[4]);
19: printf("S=%d\n",s);
20: printf("ファイル名を入力してください=>");
21: scanf("%s",fname);
22: [空欄7] /*書き込みモード"w"でファイルを開く*/
23: if(fp == NULL){
24: printf("%sをファイルオープンすることができません\n",fname);
25: exit(1); /*プログラム強制終了*/
26: }
27: [空欄8] /*ファイルに要素の二乗和の値Sを保存*/
28: fclose(fp);
29: }
問1
<解答>(2点)
scanf("%d %d %d",&x[0],&y[0],&z[0]);
scanf()を三回繰り返して読み込ませた場合も可。
可の例:
scanf("%d",&x[0]);
scanf("%d",&y[0]);
scanf("%d",&z[0]);
なお、scanf("%d %d %d\n",&x[0],&y[0],&z[0])と、\nを含めた場合、1点減点。
別解として、以下の2種類も可。この2解も正解であることを説明するには、ポインタの概念を使わなければならず、今回のテスト範囲から本来は外れている(↓の説明を参照)。
別解1: scanf("%d %d %d",x,y,z);
別解2: scanf("%d %d %d",&x,&y,&z);
(第2問 問1の別解1,2の説明(発展内容))
配列int x[10]を定義した場合、10個のint型変数をひとまとめに定義した、という意味になる。int型変数を定義したということは、コンピュータのメモリアドレス上にそれら10個の変数がそれぞれ格納されたことを意味する。これはちょうど、10個の異なるアドレスが、配列成分1つ1つの住所録の役割を果たしているようなものである。ある変数のアドレス値を求める演算子をアドレス演算子と呼び、&で表す。すなわち、&x[0]とは、変数x[0](配列x[10]の先頭成分と同値)が格納されているメモリ上のアドレス値を表す。アドレスを指し示す変数をポインタ変数と呼び、配列を定義した場合、配列の名前(この場合x)は配列の先頭成分(この場合x[0]))のアドレス&x[0]を指し示すポインタである、という決まりがある。
すなわち、
配列x[10]の名前x は &x[0] と同値である -> 従ってscanf("%d",&x[0]);とscanf("%d",x);は同じ結果となる。
では、配列int x[10]を定義した場合の&xはどのような意味となるのか。これは配列そのもののアドレスを求めていることになり、その値は、配列先頭成分のアドレス値&x[0]と同じである。
&x[0]の意味
-> 配列成分x[0](中味はint型「変数」)のアドレス
&xの意味
->配列x(中味はint型「ポインタ」)のアドレス
となり、意味は異なるがアドレス値そのものは同じである。従って、本プログラム中では、scanf("%d",&x[0]);とscanf("%d",x);とscanf("%d",&x);は同じ結果となる。
以下、第2問 問2と問3は[空欄2,3,4,5]すべてできて5点、問2のforループの回数と問3の漸化式に整合性がとれていなければ3点(問2,3別解の項参照)
問2
式(2)の漸化式を0≦n≦4の範囲で計算します。題意に沿うように[空欄2]を埋めなさい。
<解答>
n=0;n<=4;n++
問3
式(2)の漸化式を0≦n≦4の範囲で計算し、xn,yn,znを順次求めます。題意に沿うように[空欄3], [空欄4], [空欄5]を埋めなさい。
<解答>
問2の解答がn=0;n<=4;n++であるという前提では、以下の解が正解となる
[空欄3]: x[n+1]=z[n]; [空欄4]: y[n+1]=y[n]+z[n]; [空欄5]: z[n+1]=-x[n];
<第2問 問2,3の別解>
[空欄3,4,5]の漸化式をx[n]=z[n-1]; y[n]=y[n-1]+z[n-1]; z[n]=-x[n-1]とした場合、{空欄2]の解答はn=1;n<=5;n++としなければならない。
同様に、x[n+2]=z[n+1]; y[n+2]=y[n+1]+z[n+1]; z[n+2]=-x[n+1]とした場合、{空欄2]の解答はn=-1;n<=3;n++としなければならない。
以上の整合性がなされている場合5点。空欄[3,4,5]はすべて正しいが[空欄2]との整合性がとれていない場合、3点。
以下、空欄[3,4,5]1つのミスにつき1点減点。
問4
式(3)の二乗和 を計算、変数sに代入します。[空欄6]を埋めなさい。
<解答>(1点)
s=s+x[n]*x[n]+y[n]*y[n]+z[n]*z[n];
第1問 問3[空欄4,5]と同様に、s+=x[n]*x[n]+y[n]*y[n]+z[n]*z[n];としても可。
問5
「書き込みモード"w"でファイルを開く」題意に沿うように[空欄7]を埋めなさい。
<解答>(1点)
fp=fopen(fname,"w");
問6
ファイル内に、以下の表記に従って式(3)の二乗和Sを保存します。題意に沿うように[空欄8]を埋めなさい。
↓ファイル内表記 (***には本プログラムを実行した計算結果が表示される)
S=***
<解答>(1点)
fprintf(fp,"S=%d",s);
なお、fprintf(fp,"%d",s);のように、S=は無くとも可。また、"S=%d\n"と、\nを入れても可。
問7
初期値として(x0,y0,z0)=(1,2,3)を与え,本プログラムを実行したときのベクトル(x4,y4,z4)と二乗和Sの値を解答用紙に記しなさい。
<解答>(各1点、計2点)
ベクトル(x4,y4,z4)=(1,2,3)
二乗和S=100
<全体への注意点>
文の最後のセミコロン( ; )抜けミス(例: 第1問 問1 double sum,piとした場合)やカンマ( , )抜けミス(例: 第1問 問1 double sum pi;とした場合)については、それらのミスがなければ正解となる箇所についてのみ累計し、以下の基準に従い総得点から減点する。
1-2個: 減点0点
3-5個: 減点1点
6個以上: 減点2点